分子间力：液体和固体
封面图：南极的冰川，在图中，水以三种状态存在——固态、液态和气态。我们在第6章学习了气体的宏观性质与微观状态的关系。本章将了解固体和液体的宏观性质与分子间力的联系。/©Erika
在第6章我们了解到，温度越低分子热运动速度越慢。温度足够低时，分子间吸引力占主导地位，物质以凝聚态（固态、液态）存在。反过来，随着温度上升，分子的热运动将克服分子间吸引力，物质将气化。有些时候我们可以将气体视为理想气体，完全忽略分子间作用力。但对于固体和液体，我们必须考虑这种作用。
12.1 分子间作用力
在第6章学习气体的性质时，我们注意到低温、高压下，气体的行为将偏离理想气体。当这种作用强于热能时，气体就会液化。液体的体积远小于气体，所以液体中分子的平均距离也小于气体状态。我们还学习了一种描述实际气体状态的方程——范德华方程：$p=\frac{nRT}{V-nb}-\frac{n^2a}{V^2}$。范德华方程与理想气体状态方程有两处不同，第一处使用系数$b$修正体积项，第二处使用系数$a$修正气压项。我们本章将要学习的分子间力——范德华力——对气体行为的影响便通过$\frac{n^2a}{V^2}$进行修正。
另外，分子的两个性质——偶极矩（见10.7节）和极化率（见9.7节）——是描述分子间力的物理基础。在开始分子间力的学习之前，我们先复习一下分子的这两个性质。
偶极矩和极化率
当分子中正负电荷中心不重合时，就存在偶极矩。判断分子是否存在偶极矩的一种方法是观察化学键的偶极矩，并考虑它们的大小与方向。例如CCl4和CHCl3分子，前者不具有偶极矩，因为四根极性的C—Cl键的偶极矩相互抵消。
CCl4和CHCl3分子的静电势图，以及C—Cl键的偶极矩方向。这两个分子都含有极性共价键，但CCl4的偶极矩为0。
另一个性质是极化率α，其用来衡量物质在外界电场作用下被极化的能力。极化率越大，电场会让电子更容易『偏离』原来的位置。一般来说，极化率和分子体积有关，体积越大极化率越大，所以极化率也通常以体积单位表示。三氯甲烷的极化率为8.13×10−24 cm3，而四氯化碳的极化率为1.00×10−23 cm3。
具有偶极矩的分子是极性分子，其相比于非极性分子具有更多种类的分子间力。
偶极-偶极相互作用
我们将要了解的第一种分子间力是偶极-偶极相互作用，只有两个极性分子之间才存在这种作用。极性分子具有永久偶极矩，一个分子倾向于把带正电荷的部分对准另一个分子带负电荷的部分。分子间的这种有序排序将带来更多的分子间力，使物质更容易保持为固体或液体。
极性分子有序排列，使得偶极矩头对尾。这种排列增加了分子间作用，使分子更难挣脱束缚变为气体。
考虑CF4和CHF3两种物质，CF4的沸点是−128 °C，而CHF3的沸点是−81 °C，要高大约40 °C。这说明CHF3的分子间具有更强的作用，这种作用包括如下两种：
- 偶极-偶极相互作用（取向力）：例如CHF3的偶极矩头对尾，如上图中的那样。
- 偶极-诱导偶极相互作用（诱导力）：一个极性分子的偶极矩会使得相邻分子的偶极矩发生变化，即引起相邻分子的极化。见下图所示。
一个极性分子吸引旁边分子的电子，使其极化产生诱导偶极矩。
一个极性分子吸引旁边分子的电子，使其极化产生诱导偶极矩。
因旁边极性分子导致的偶极矩称为诱导偶极矩，极性分子的偶极矩与诱导偶极矩头对尾，进一步增加分子之间的作用力。
色散力
非极性分子不存在上述两种相互作用，所以很多非极性分子具有较低的沸点——但它们并非不能液化。如果温度足够低，He、O2、N2等物质也会变为液态。即使是非极性分子，也存在一种很弱的相互作用。这种作用非常弱，只有在很低的温度下，分子的运动才能被这种相互作用所束缚。
我们知道分子中电子无时无刻不在运动，电子的移动会让非极性分子产生瞬时偶极矩。简单来说，电子可能集中在分子的某个区域，导致正电荷中心（由原子核位置决定）和负电荷中心（由电子位置决定）不重合，从而产生瞬时偶极矩。
当一个分子产生瞬时偶极矩，其可以极化旁边的分子，产生诱导偶极矩。这样一来就产生了瞬时偶极-诱导偶极相互作用。这一名字太长，所以一般我们把这种作用称为色散力(dispersion force)或伦敦力(London force)，纪念通过理论推导出该作用表达式的弗里茨·伦敦(1900-1954)。取向力、诱导力和色散力都属于范德华力，
一般来说，极化率越大，分子产生的瞬时偶极矩越强，也越容易被极化。所以极化率越大色散力也越强，该分子组成的物质沸点也越高。极化率粗略地和分子量成正比，因为分子量越大电子数也越多，一般来说电子云也越大、越容易被极化。所以我们也说分子量越大沸点越高，这是一个经验的判断方法。例如He具有所有物质中最低的沸点——4 K，而氡的沸点为211 K。
例题
便携打火机中使用的燃料是丁烷(C4H10)，而丙酮(C3H6O)是常用的有机溶剂。何者具有更高的沸点？
解答
丙酮和丁烷的分子量接近，但丙酮中有极性较大的C=O键，因此丙酮沸点更高。
练习
按沸点升高的顺序排列：C8H18、CH3CH2CH2CH3、(CH3)3CH、C6H5CHO。
氢键
那么H2O和H2S的沸点何者更高？我们知道水在室温下是液体，而硫化氢是气体。但水的分子量却小于硫化氢。这说明水分子间存在某种比范德华力更强的相互作用。下图展示了主族元素氢化物的沸点，从图中可以看出，沸点『异常』的除了H2O外，还包括NH3和HF。
NH3、H2O和HF，这三个第二周期元素氢化物的沸点存在『异常』，相比于其他氢化物要高很多。
NH3、H2O和HF，这三个第二周期元素氢化物的沸点存在『异常』，相比于其他氢化物要高很多。
N、O、F的共同特征之一是大的电负性，这意味着N—H、O—H或F—H具有较大的极性，也具有较大的偶极矩。考虑两个HF形成的偶极对H—F···H—F，由于H原子半径很小，所以两个分子可以靠得很近，产生强烈的偶极-偶极作用。如此短的F···H距离，使得这两个原子间存在少许的化学键成分，尽管其相比于H—F要弱许多。我们把这种形如X—H···Y−的分子间作用称为氢键。
氢原子与高电负性原子X结合，所以H原子带正电。H原子被旁边的带负电荷的Y−吸引，我们把X—H称为氢键给体，因为它提供了带正电荷的氢原子，而Y−称为氢键受体，其接受了氢原子。氢键的能量大约在15~40 kJ mol−1，尽管氢键一般比范德华力要强，但其不属于化学键。共价单键的键能大于150 kJ mol−1。
水中的氢键
水是生命之源，在上一小节的图表中我们看到H2O的沸点相当的高——H2Te的分子量是129.6，是H2O的七倍多，但沸点仍远低于H2O。分子量相近，同时也能形成氢键的NH3和HF其沸点也比H2O要低。
如果我们观察冰的微观结构，就能知道原因。水分子有两个氢原子，可以作为氢键给体形成两个氢键。水分子有一个氧原子，由于氧的高电负性，其带有负电荷，可以作为氢键受体。最后结果是，冰中每个水分子参与形成4根氢键，而HF和NH3的晶体中每个分子参与形成的氢键数量没有H2O中那么多，因此沸点也不如H2O高。
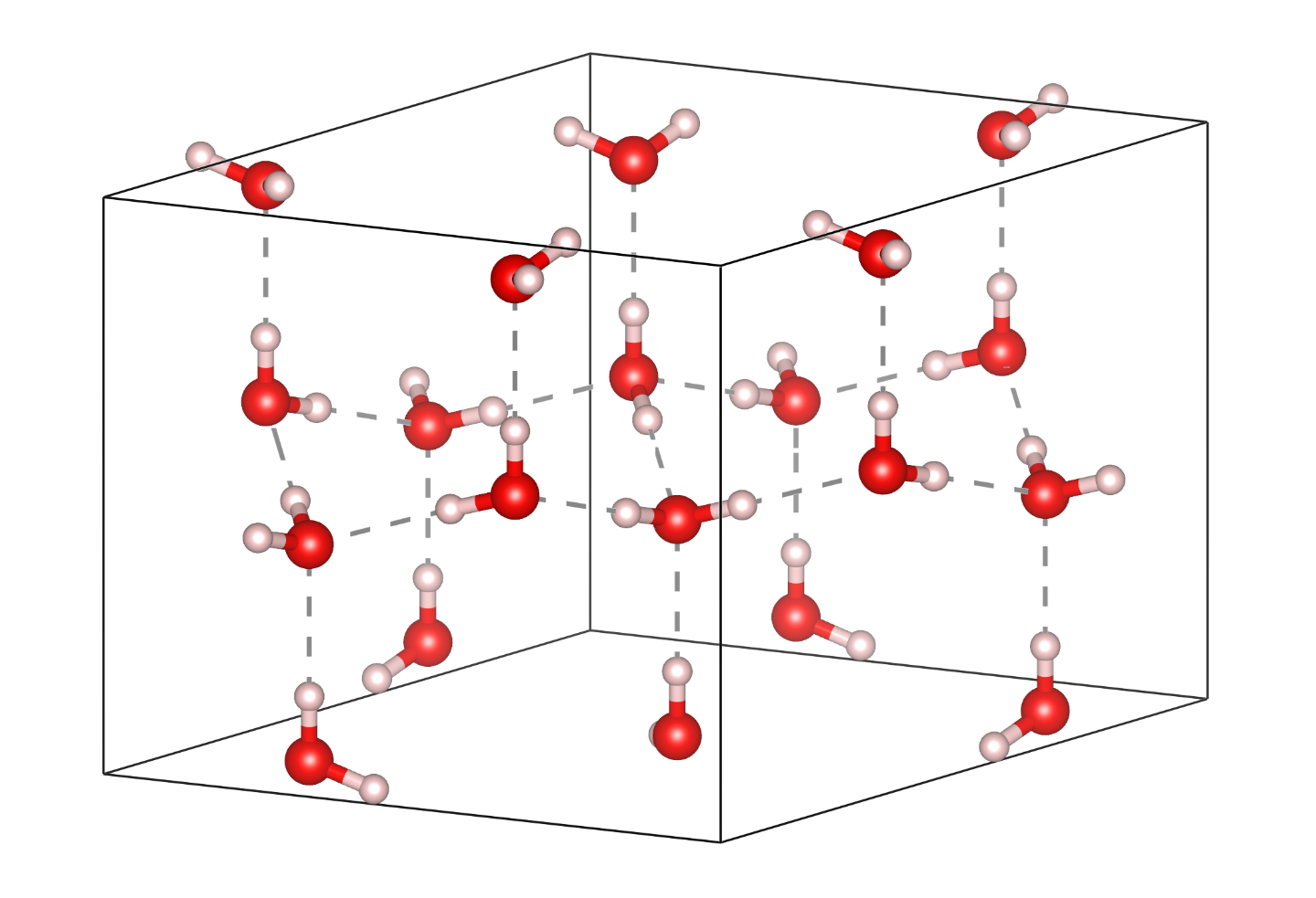Ih冰的微观结构，这是冰在通常状况下的晶体结构。每个水分子有两个H原子，作为氢键给体与周围的两个水分子形成氢键。且每个水分子同时作为氢键受体，形成两个氢键。所以每个水分子参与形成四根氢键。
冰有另一个奇怪的性质——冰块浮在水面上而不是沉下去，这表明冰熔化后体积减少（密度增加）。观察冰的结构我们发现，水分子用氢键形成的框架结构具有较多的空隙。冰熔化后部分氢键被破坏，水分子能更加紧密的接触，所以密度增加。随着温度进一步上升，分子热运动加剧，分子间距进一步增大密度又开始减少，最终导致水在3.98 °C下具有最高的密度。这一性质使得生命在冬季的淡水湖中仍能生存，湖水表面结冰后会隔绝进一步的热量损失，使得底层水保持约4 °C的温度而不结冰。如果冰的密度大于水，那么冰将会沉入底部，最终所有的湖水结冰，鱼类、小型底栖动物和水生植物都将冻住而无法越冬。
氢键对物质性质的影响
很多物质的性质与氢键有关，除了水之外，乙酸也是一个例子。乙酸分子倾向于通过氢键结合为二聚体，在液态和气态中都是如此。所以乙酸蒸发的时候，只有少数氢键发生断裂，所以乙酸具有较低的蒸发焓。
两个乙酸分子通过氢键形成二聚体。
两个乙酸分子通过氢键形成二聚体。
液体的粘度受到分子间力的影响，具有较强分子间作用力的物质具有较高的粘度，因为液体必须克服这些作用力才能相互移动。氢键通常强于范德华力，如果一个分子能形成一个甚至多个氢键，可以预计其具有更低的粘度。蜂蜜在室温下是粘稠的液体，其主要成分是果糖、葡萄糖（以及水）。果糖和葡萄糖和水分子之间均能形成氢键，液体的粘度也与分子之间形成氢键的数量有关。可以预计，丙三醇（甘油）比乙二醇粘度更大，乙二醇粘度大于乙醇。
蜂蜜的主要成分是果糖(fructose)和葡萄糖(glucose)，它们都包含很多羟基，可形成氢键，具有较大的分子间作用力。所以蜂蜜是一种黏稠的液体。
蜂蜜的主要成分是果糖(fructose)和葡萄糖(glucose)，它们都包含很多羟基，可形成氢键，具有较大的分子间作用力。所以蜂蜜是一种黏稠的液体。
分子内氢键和分子间氢键
上述例子都涉及到分子间的氢键，但氢键也可以在分子内部形成。分子内氢键不会增加分子间作用力，这会影响物质的性质。一个典型的例子是邻硝基苯酚和对硝基苯酚。邻硝基苯酚形成分子内氢键，分子间作用主要是范德华力。对硝基苯酚可形成分子间氢键，其分子间作用更强，所以对硝基苯酚具有更高的熔点和沸点。
邻硝基苯酚和对硝基苯酚的结构，邻硝基苯酚形成分子内氢键，而对硝基苯酚形成的是分子间氢键。邻硝基苯酚具有更低的熔点和沸点，因为其具有更弱的分子间力。
邻硝基苯酚和对硝基苯酚的结构，邻硝基苯酚形成分子内氢键，而对硝基苯酚形成的是分子间氢键。邻硝基苯酚具有更低的熔点和沸点，因为其具有更弱的分子间力。
范德华力总结
如何判断色散力、诱导力和取向力所占的比例？可参考如下几条规则：
- 所有分子之间都存在色散力。色散力的强度随着分子体积的增加而增加，且与分子形状也有关系。
- 只有极性分子才具有诱导力和取向力，分子极性越强取向力越强，所占比例越大。
- 弱极性分子的分子间力以色散力为主，强极性分子以取向力为主。
- 大的非极性分子之间的色散力可能大于小的极性分子之间的取向力。
下表中有一些数据，数据将范德华力粗略分为色散力和偶极引起的力（即诱导力和取向力之和）。从表格中可以看出，从HCl到HBr再到HI，其色散力所占比例越来越大。
| 分子量/u | 极化率/cm−3 | 偶极矩/D | 色散% | 偶极% | |
|---|---|---|---|---|---|
| F2 | 38.00 | 1.38×10−24 | 0 | 100 | 0 |
| HCl | 36.46 | 2.63×10−24 | 1.08 | 77.4 | 22.6 |
| HBr | 80.91 | 3.61×10−24 | 0.82 | 93.6 | 6.4 |
| HI | 127.91 | 5.44×10−24 | 0.44 | 99.2 | 0.8 |
表格中没有给出HF的数据，因为HF中的氢键作用远强于范德华力。你可能对如何计算色散和偶极的百分数感兴趣，具体公式在本章一道习题中有。
12.2 液体的一些性质
液体很多性质与分子间作用力有关，本章将介绍液体的表面张力、粘度、以及液体气化过程的一些热力学性质。
表面张力
一些密度大于水的物体有时也能浮在水面上，例如下图中的金属曲别针。这有些违反常理，这一现象说明存在某种力，托起了金属。这种力源于水的表面张力(surface tension)。
漂浮在水面上的曲别针，钢的密度大于水，曲别针没有沉入水底说明存在某种力托起了物体。
考虑一杯水不同部位水分子受到的分子间作用，在水-空气界面处的水分子所与内部分子相比，受到更少的分子间力，因为其邻近的分子更少。因此内部分子的能量更低，而表面分子的能量更高。从宏观上看，就是液体表面积越大，能量越高。因此液体倾向于保持尽可能小的表面积，如果液体表面积增加，就需要外界对其做功。曲别针能悬浮在水面上，就是因为需要能量才能让水完全没过曲别针表面。
在水-空气界面处的水分子所与内部分子相比，受到更少的分子间力，因为其邻近的分子更少。因此内部分子的能量更低，而表面分子的能量更高。
在水-空气界面处的水分子所与内部分子相比，受到更少的分子间力，因为其邻近的分子更少。因此内部分子的能量更低，而表面分子的能量更高。
表面张力是增加液体表面积所需要的能量或功，通常用希腊字母γ表示，其单位为J m−2。一般来说表面张力随温度升高而降低，因为分子热运动使得分子间力变得不那么重要，所以增加液体表面积所需的功减少。另外表面活性剂（例如肥皂）也会减少溶液的表面张力，有关表面活性剂的内容会在本章后面学习。
当液体在固体表面展开形成薄膜时，我们说液体浸润了表面。液体能否浸润表面取决于液体内部分子间作用——称为内聚力(cohesive force)——和液体与表面的分子间作用——称为粘附力(adhesive force)——的强度。如果内聚力强于粘附力，那么液体将不会浸润固体表面。反之，液体将浸润固体，因为将液体展开所需要克服的内聚力由粘附力所做的功提供。
水会浸润很多固体表面，例如玻璃、织物。但如果我们在玻璃上涂上一层油，水就不会浸润玻璃。在织物上使用特定涂层，可以获得防雨的衣物。荷叶表面具有疏水性，雨水落到荷叶上会形成水珠，风吹动就能让水珠滚落，并带走灰尘和污泥，从而起到自洁的效果。利用荷叶效应，可以用于生产具有自洁功能的建筑材料，如天窗玻璃板。
荷叶效应，是指莲叶表面具有超疏水性以及自洁的特性。©Peng Luyao
如果我们仔细观察浸润表面的水珠以及不浸润的水珠，会发现它们与表面的接触角并不一样。当接触角小于90°时，我们称液体浸润表面，反之则不浸润。如果液体在垂直的管道中浸润表面，那么在重力和表面张力的共同作用下，液体与空气的界面是凹液面，反之为凸液面。水可以浸润洁净的玻璃，而汞不能。因为汞原子之间的金属键很强，其内聚力大于粘附力。
试管中的汞具有凸液面，而水具有凹液面。/©karabekirus CC BY-SA 2.0
如果将一根毛细管插入水中，我们会观察到毛细管中的水柱高于外液面，这一现象称为毛细作用。海绵、纸张等物体浸泡在水中，水会通过内部的毛细管上升。水渗入土壤也与毛细作用有关，水分会从潮湿的土壤转移到更干燥的地方。而具有很强内聚力的液体——汞——将不表现出毛细管上升。相反，毛细管中的汞液面将低于外部。
一根毛细管和一张滤纸放在被染色了的水中，毛细管中的液面高度高于毛细管外。/©Lars Egil Helseth CC BY-SA 3.0
粘度
另一个与分子间力有关的液体性质是粘度(viscosity)，即液体抵抗流动的能力。分子间力越强，液体粘度越大。当液体流动时，一部分液体会相对于另一部分液体发生移动，这一过程需克服液体内部的摩擦力。低粘度的液体很容易流动，如水、乙醇。而高粘度液体流动速度很慢，如糖浆、甘油。某些液体的粘度极其巨大，例如沥青，沥青从漏斗中滴落一滴将花费约10年的时间。
沥青滴落实验装置。沥青是粘度极高的液体，其被放置在漏斗中。每滴沥青滴落需要约10年的时间，这一实验从1927年开始进行，最近的一次滴落是2014年4月，为第9滴。/©John Mainstone CC BY-SA 3.0
一般来说温度越高粘度越低，因为高温导致的分子热运动动能会克服分子间作用力。粘度的SI单位为Pa s，有时也用泊松(P, poise)表示粘度，1 P = 0.1 Pa s。
气化焓
在第6章有关分子动理论的章节，我们了解到分子的速度和动能具有宽广的分布。在第7章我们了解到，动能远高于平均值的分子可以克服分子间吸引力并从液体表面逃逸到气态。液体变为气态的过程称为气化或蒸发，有如下的方法促进液体的气化：
- 升高温度——增加分子的动能以克服分子间吸引力。
- 降低分子间力强度——让分子所需要克服的分子间吸引力减少。
- 增加液体表面积——让更多分子处在表面。
由于蒸发走的分子会携带更多动能逃逸，这将导致留在液体中分子的平均动能降低，使液体温度下降。这能解释为何酒精喷洒在手上会有清凉感，以及为何刚刚运动完在空气流动处会感觉更凉爽。在恒定温度和恒定压力下蒸发一摩尔液体所吸收的热量称为蒸发焓，$\Delta_\text{vap}H$。$\Delta_\text{vap}H$通常用kJ mol−1表示，由于蒸发过程是吸热的，所以$\Delta_\text{vap}H$始终为正值。
| 液体 | $\mu$, D | $\alpha$, 10−25 cm3 | $\Delta_\text{vap}H$, kJ mol−1 | bp, °C |
|---|---|---|---|---|
| 二甲醚 | 1.30 | 52.9 | 18.5 | −24.8 |
| 乙醚 | 1.10 | 102 | 27.1 | 34.5 |
| 甲醇 | 1.70 | 32.0 | 37.4 | 64.6 |
| 乙醇 | 1.69 | 54.1 | 42.3 | 78.3 |
| 水 | 1.85 | 14.5 | 44.0 | 100 |
上表列出了一些常见液体的$\Delta_\text{vap}H$，其数值与分子间吸引力有关。乙醇具有和二甲醚一样的分子量，乙醚的分子量甚至大于乙醇，但乙醇反而具有更高的沸点蒸发焓。这表明氢键对蒸发焓有较大影响，因为气化过程会大大增加分子间距离，氢键会被破坏，所需要更多的能量。水分子之间能形成更多的氢键，其蒸发焓大于甲醇和乙醇。
综上所述，存在氢键时，$\Delta_\text{vap}H$和沸点随氢键数增加而增加。不形成氢键时，$\Delta_\text{vap}H$和沸点随着分子极化率的增加而增加。
物质从气体转变为液体的过程称为液化，液化是气化的逆过程。因此$\Delta_\text{vap}H$一定为负，这是个放热过程。这也能解释为何蒸汽烫伤比热水烫伤通常严重得多，因为水蒸气液化的过程会放出大量的热。
例题
正常沸点，1 atm下的0.750 L水蒸气在略低于沸点的表面液化，计算这一过程的焓变。
解答
液化后的水的温度略低于沸点，这一步的热量变化可忽略。根据气体状态方程，计算出水的物质的量$n=\frac{pV}{RT}$ = 0.0245 mol。因此$\Delta H$ = 0.0245 × −44.0 = −1.08 kJ。
练习1
3.20 g乙醇在298 K下蒸发，计算这一过程的焓变。
练习2
100 g 373 K下的水蒸气与100 g 0°C的液体水混合，所得水的温度是多少？水的比热容近似为4.20 J g−1 K−1。
蒸气压
潮湿的衣服经过一段时间后会晾干，水以气体的形式进入到空气中。而一些水果会用塑料袋包裹着出售，这样能保持水润而不干燥。南方梅雨季节，地下室的瓷砖会『出汗』，这是空气中的水蒸气在表面液化所致。
在液体表面，时刻存在着两个过程：分子气化而脱离液体，以及气体中的分子进入液体。这两个过程最终会达到动态平衡，即蒸发和液化的速率相同，与液体处动态平衡状态的蒸气所施加的压力称为蒸气压(vapor pressure)。在常温下具有较高蒸气压的液体称为挥发性液体，例如乙醚、乙醇、水。而蒸气压很低的液体称为非挥发液体，例如甘油、硅油。
液体是否具有挥发性取决于分子间力的强度，分子间作用力越弱，液体越容易挥发（蒸气压越大）。乙醚和丙酮具有较大的挥发性，在25 °C下的蒸气压分别为71.2和30.8 kPa。水具有中等的挥发性，25 °C蒸气压为3.17 kPa。虽然大家对汞谈之色变，但汞的蒸气压并不大，在25 °C下为0.24 Pa，可以认为是非挥发性液体。即使少量的汞蒸气也是有害的，室温下饱和的汞蒸气就已具有毒性，不能因为其挥发性很低就放松警惕。
一些常见溶剂的蒸气压曲线，与粗线(101.325 kPa)相交处的横坐标就是正常沸点。
一些常见溶剂的蒸气压曲线，与粗线(101.325 kPa)相交处的横坐标就是正常沸点。
特定液体的蒸气压只与温度有关，而与液体的量无关。如果分压小于蒸气压，液体便会持续蒸发。因此即使在远低于沸点的温度下，水也能蒸发进入空气。蒸气压与温度的函数图称为蒸气压曲线，一些液体的蒸气压曲线如上图所示，随着温度升高蒸气压将增加。
有一种简单的办法测量蒸气压：在水银气压计的管内注入少量待测液体，测量水银柱的高度下降。该方法的精确度并不高，而且无法测量非常高或非常低的蒸气压。实验室中会使用一些其他方法测量液体蒸气压，例如使用精密的气压计测量正在沸腾的液体上方的气压。本小节例题提供了一种测量极低蒸气压的方法。
在标准大气压下，水银气压计中汞柱的高度为760 mm。往其中加入一些挥发性液体，汞柱高度会下降，下降的高度就是当前温度下液体的蒸气压（以mmHg为单位）。
在标准大气压下，水银气压计中汞柱的高度为760 mm。往其中加入一些挥发性液体，汞柱高度会下降，下降的高度就是当前温度下液体的蒸气压（以mmHg为单位）。
例题
1360 °C下体积为113 L的氦气缓慢通过一些融化的银样品，气体被银蒸气饱和。氦气通过后，银的质量减少了0.120 g，计算1360 °C下银的蒸气压。
解答
因为蒸发的银非常少，我们假定蒸发后气体体积仍为113 L，因此0.120 g银在113 L气体中饱和，Ag的物质的量为1.11 mmol，因此：$p=\frac{nRT}{V}$ = 0.00111×8.314×1633÷113 = 0.133 kPa。
练习
在25.0 °C下测量己烷上方的蒸气密度，为0.701 g L−1。计算己烷在25.0 °C下的蒸气压。
水的蒸气压见下表，在一些题目中你会用到这些数据。
| 温度/°C | 蒸气压/kPa | 温度/°C | 蒸气压/kPa | 温度/°C | 蒸气压/kPa |
|---|---|---|---|---|---|
| 0.0 | 0.611 | 29.0 | 4.00 | 94.0 | 81.4 |
| 10.0 | 1.23 | 30.0 | 4.25 | 95.0 | 84.5 |
| 20.0 | 2.34 | 40.0 | 7.38 | 96.0 | 87.7 |
| 21.0 | 2.49 | 50.0 | 12.3 | 97.0 | 90.4 |
| 22.0 | 2.64 | 60.0 | 19.9 | 98.0 | 94.3 |
| 23.0 | 2.81 | 70.0 | 31.2 | 99.0 | 97.8 |
| 24.0 | 2.99 | 80.0 | 47.4 | 100.0 | 101 |
| 25.0 | 3.17 | 90.0 | 70.1 | 101.0 | 105 |
| 26.0 | 3.36 | 91.0 | 72.8 | 102.0 | 109 |
| 27.0 | 3.56 | 92.0 | 75.6 | 110.0 | 143 |
| 28.0 | 3.77 | 93.0 | 78.5 | 120.0 | 199 |
例题
50.0 °C下，0.132 g H2O放在一个525 mL的容器中。达到平衡后，容器中水的状态是什么？
解答
若一个50.0 °C下的525 mL容器充满饱和水蒸气，水的质量为：$m=\frac{pVM}{RT}$ = 12.3×0.525×18.016÷8.314÷323.15 = 0.043 g。因此水以气体和液体的状态存在。
练习
将上述容器加热至80.0 °C，所有的水都会气化吗？
如果你搜索资料，查阅一些液体的蒸气压。除了水、汞等少数液体外，不太可能获得类似于上表的蒸气压表格。而通常查找到的是蒸气压与温度的数学方程。这样的数学方程只需要少数几个参数进行描述，而表格需要整整一页的篇幅。描述蒸气压最常见的的方程的形式为：
其中$A$和$B$是参数。从方程我们可以看出，蒸气压$p$的对数与温度$T$的倒数是关系是线性的。一些液体的$\ln p$与$1/T$的关系如下图：
一些液体$\ln p$（以kPa为单位）与$1/T$（以K为单位）的关系，近似为一条直线。
一些液体$\ln p$（以kPa为单位）与$1/T$（以K为单位）的关系，近似为一条直线。
参数$A$的值与液体的气化焓有关，$A=\Delta_{\text{vap}}H/R$，其中$R$为气体常量。当方程涉及两个不同温度时，我们可以消去参数$B$，获得被称为克劳修斯-克拉佩龙(Clausius–Clapeyron)方程的关系式：
例题
已知30.0和40.0 °C下水的蒸气压分别为4.25和7.38 kPa，计算35.0 °C下水的蒸气压。
解答
首先利用已知数据计算$\Delta_{\text{vap}}H$：
$\Delta_{\text{vap}}H=-\frac{R\ln\left(\frac{p_2}{p_1}\right)}{\left(\frac{1}{T_2}-\frac{1}{T_1}\right)}$ = 43.56 kJ mol−1 然后利用$\Delta_{\text{vap}}H$和任何一个温度下的蒸气压，计算35.0 °C下水的蒸气压：
$p_2=p_1 e^{-\frac{\Delta_{\text{vap}}H}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)}$ = 5.63 kPa 练习
异辛烷(C8H18)是汽油的成分之一，其沸点为99.2 °C，其蒸发焓为35.76 kJ mol−1。计算异辛烷在25 °C下的蒸气压，以kPa计。
沸腾和沸点
在敞口容器中加热液体时，液体会在恒定的温度下气化。气化并不只在表面发生，气泡主要在液体内部产生，并上升到表面。我们常把正在沸腾的水称为『滚水』，其形象地描述了气泡冒出水面的过程。沸腾过程吸热，吸收的热量用于将液体转化为蒸气。沸腾过程温度是恒定的，在一个大气压下沸腾的温度称为正常沸点。液体的正常沸点可以通过蒸气压曲线与1 atm的交点确定。
液体的沸点与压力有关，在更高的压力下沸腾需要更高的温度，反之低压下的沸点更低。青藏高原（平均海拔约4000 m）的气压为60 kPa，在该气压下水的沸点约为85 °C。在更低的沸点下烹饪需要更长的时间，高压锅可以抵消高海拔带来的影响。高压锅中的压力高于大气压，其内部的食物可以达到比水沸点更高的温度。所以在高原地区居民的厨房中能经常能看高压锅。
高压锅顶部有一个泄压阀，内部压力可以保持在约2个大气压。在此压力下，水的沸点约为120 °C，因此高压锅中烹饪的食物熟得更快。/©AnnRve
例题
按照沸点增加的顺序排列：CCl4、Cl2、ClNO、N2。
解答
这些物质中只有ClNO是极性分子。四个分子的分子量分别为：154、71、65.5、28。由于ClNO具有极性，其沸点应该高于Cl2。所以顺序为：N2、Cl2、ClNO、CCl4。
练习
按照沸点增加的顺序排列：Ne、He、Cl2、(CH3)2CO、O2、O3。
临界点
如果在一个封闭容器中加热液体，会发生什么？如果容器非常坚固，能耐受很大的压力，我们会观察到无论温度多高，液体也不会沸腾。从蒸气压曲线可以看出，温度增加蒸气压会迅速上升，甚至能达到大气压的数十倍。温度越高，液体的密度越低（剧烈的分子热运动会增大分子间距离）。而压力越大，气体的密度越大。最终在某个温度和对应的压力下，液体和气体具有完全相同的密度，它们之间将变得不能区分，此时便达到了临界点(critical point)。一些物质的临界温度与临界压力见下表：
| 物质 | $T_\text{c}$ / K | $p_\text{c}$ / bar | 物质 | $T_\text{c}$ / K | $p_\text{c}$ / bar |
|---|---|---|---|---|---|
| H2 | 33.3 | 12.8 | CO2 | 304.2 | 72.9 |
| N2 | 126.2 | 33.5 | HCl | 324.6 | 82.1 |
| O2 | 154.8 | 50.1 | NH3 | 405.7 | 112.5 |
| CH4 | 191.1 | 45.8 | SO2 | 431.0 | 77.7 |
| H2O | 647.3 | 218.3 |
只有在低于临界温度和临界压力的情况下，物质才有可能被液化。表格左侧的四种物质的临界温度均低于室温，这些气体在室温下无法液化。所以氧气钢瓶中储存的是高压气体而不是液化氧气。二氧化碳的临界温度比室温稍高，在冬天摇晃二氧化碳灭火器，能听到内部液体流动的声音。
12.3 固体的一些性质
在第2章我们已经了解到了一些固体的性质，例如延展性、导热性。我们本节将学习更多固体的性质。
熔点与熔化热
晶体中的微粒在空间中规律地排列，微粒可以是原子、离子或分子。当固体被加热时，微粒的热运动逐渐增加，最终达到破坏晶格有序结构的温度。此时微粒之间可以相互滑动，固体失去其形状并变为液体。这个过程称为熔化，发生熔化的温度就是熔点(melting point)。相反，如果液体降温，其将凝固为固体，发生的温度称为凝固点(freezing point)。固体的熔点与其液体的凝固点相同，在此温度下固体和液体可以平衡共存。如果我们加热处于平衡状态的固液混合物，物质吸收的热量将用于使更多固体熔化，而不是用来提高液体的温度。因此熔化过程温度保持不变，直到所有固体都已变成液体，系统温度才能继续升高。相反，如果从平衡状态的固液混合物吸收热量，也只有当所有液体都已凝固，系统温度才能降低。
| 物质 | 熔点 | $\Delta_\text{fus}H$/kJ mol−1 |
|---|---|---|
| 汞，Hg | −38.9 | 2.30 |
| 钠，Na | 97.8 | 2.60 |
| 甲醇，CH3OH | −97.7 | 3.21 |
| 乙醇，CH3CH2OH | −114 | 5.01 |
| 水，H2O | 0.0 | 6.01 |
| 苯甲酸，C6H6COOH | 122.4 | 18.08 |
| 萘，C10H8 | 80.2 | 18.98 |
熔化固体所需的热是熔化焓$\Delta_\text{fus}H$，上表列出了一些常见物质在1 atm下的熔化焓和熔点。大家最熟悉的熔点应该是冰的，其在0 °C下熔化为水。这是在标准大气压下与空气接触的冰水混合物的温度，也是摄氏零度的定义。水的熔化焓为6.01 kJ mol−1，其表示的为：
如何确定某个物质的熔点？最简单的办法是测量固液混合物的温度。我们可以取一些液体，不断移去体系的热量，并测量温度与时间的关系。随着液体开始冷却，温度逐渐下降，直到开始凝固。接下来的一段时间温度保持在凝固点不变，直到所有液体都凝固，然后温度再次下降。这样我们就获得称为冷却曲线的图，见下图（左）。我们也可以反过来加热固体，获得的会是加热曲线，见下图（右）。
水的凝固曲线（左）和加热曲线（右）示意图。左图中存在一段虚线，其指出水冷却过程可能存在过冷现象。
水的凝固曲线（左）和加热曲线（右）示意图。左图中存在一段虚线，其指出水冷却过程可能存在过冷现象。
很多时候，即使液体温度已经下降到凝固点以下，仍然没有固体产生，这种现象称为过冷。要产生固体必须形成晶核，而成核的方式可分为均相成核和异相成核。均相成核是液体自发形成固体微粒的过程，而异相成核是固体在惰性颗粒（杂质）表面析出的过程。如果液体很纯净，杂质很少，液体就很容易过冷，因为均相成核通常是缓慢的。过冷的液体一旦开始凝固为固体，温度便回升到正常凝固点，可通过温度的回升判断是否存在过冷现象。
升华
和液体一样，固体表面也有微粒能挣脱分子间作用而脱离。由于固体内作用力通常强于液体，固体一般不具有液体那样强的挥发性。固体直接变为气体的过程称为升华(sublimation)，而气体变为固体的过程称为凝华(deposition)。当固体和气体平衡共存时，此时的压力称为升华压，温度为升华点。升华焓$\Delta_\text{sub}H$是将固体转化为蒸气所需的热量，根据盖斯定律，某一温度下的升华焓等于熔化焓$\Delta_\text{fus}H$和蒸发焓$\Delta_\text{vap}H$之和，也就是：
升华压与温度的函数称为升华曲线，和蒸发过程一样，升华压与温度的关系也能用克劳修斯-克拉佩龙方程描述。
冰和干冰都是我们熟悉的可以升华的物质。中国北方大部分区域冬天最高气温低于0 °C。但积雪仍然可以从地面消失，此时雪直接升华为水蒸气。冰在0 °C下的升华压为0.61 kPa，如果空气中水的分压小于该数值，冰就可以升华。
碘可通过升华的方式提纯，在烧杯顶部放一个口径略大的圆底烧瓶，烧瓶内装有冷水。往烧杯中加入少许不纯的碘，加热烧杯，碘升华后在烧瓶底下凝华，得到更纯的碘。/©Stanislav.evyhosteny CC-BY-SA 4.0
12.4 相图
一个刚性容器中只含有某种物质，我们测量容器内部的温度和压力，并记录当前物质的状态。对于低温、高压下的物质，我们预计其应该以固态的形式存在（红点）。而高温低压下的物质预计会以气态的形式存在（褐点）。在中等的温度和压力下则可能以液体的形式存在（蓝点）。
在假想的多次实验中，我们测量特定温度与压力下物质的状态，并将物质状态用不同颜色的点记录，并绘制在二维平面上。在高温低压的情况下物质以气态存在，低温高压下物质以固态存在，而中等的温度和压力下物质可以以液体的形式存在。
在假想的多次实验中，我们测量特定温度与压力下物质的状态，并将物质状态用不同颜色的点记录，并绘制在二维平面上。在高温低压的情况下物质以气态存在，低温高压下物质以固态存在，而中等的温度和压力下物质可以以液体的形式存在。
描述物质存在的状态与温度、压力等条件之间关系的图形称为相图(phase diagram)。相图可以告诉我们，在特定的温度和压力下，物质以何种状态存在：其可能为单相，或者两种物态平衡共存，甚至是三个物态平衡共存。在本节我们将以几个常见物质为例来展示相图。
碘的相图
下图展示了较低压力范围内碘的相图，带有网格线的刻度给出了相图中的几个具有特定含义的点。它们为：
- 在20 °C下，碘的升华压为0.027 kPa
- 碘的三相点(triple point)为113.5 °C和12.1 kPa，在这个温度和压力下，碘的固态、液态、气态三相可以共存。
- 正常大气压下碘的熔点为113.7 °C，而正常大气压下碘的沸点为184.3 °C。碘在大气压下的熔点和三相点非常接近，这表明其熔点受压力的影响不大。
- 碘的临界点为546 °C和11.7 kPa。
碘的相图，注意纵坐标（压力）并不是线性的。在较低压力范围内（10 atm以内），碘的熔点基本不受压力影响，而升华或气化过程的温度受压力的影响很大。
碘的相图，注意纵坐标（压力）并不是线性的。在较低压力范围内（10 atm以内），碘的熔点基本不受压力影响，而升华点或沸点受压力的影响很大。
尽管上图中固-气的分界线以及液-气的分界线看起来是连续的，但如果我们按比例绘制，会发现它们实际上并不连续。我们已经学习了克劳修斯-克拉佩龙方程，利用上图中的数据，可以计算出碘的升华焓和气化焓分别为61.5 kJ mol−1，以及44.1 kJ mol−1。升华焓大于气化焓，它们的差就是熔化焓。碘在室温附近的升华压非常小，而在高温下的蒸气压很大，因此无法使用线性的坐标绘制，这也是为何上图纵坐标使用了对数的比例。
二氧化碳的相图
现在我们来看看二氧化碳的相图，它与碘的相图有两个地方显著不同。第一是CO2的三相点压力高于1 atm，因此常压下CO2不会以液体存在，在敞开的容器中放置一块低温下的干冰（固态CO2），它会在恒定−78.5 °C下升华，而不产生液体，这也是为何其叫做干冰。
二氧化碳的相图。与碘不同的是，二氧化碳的熔点随压力有变化，压力越大熔点越高。
二氧化碳的相图。与碘不同的是，二氧化碳的熔点随压力有变化，压力越大熔点越高。
在高于5.1 atm的压力下有可能获得CO2液体，例如在CO2灭火器中。有趣的是，如果你使用CO2灭火器，喷出的将会是干冰和气态CO2的混合物。因为CO2(l)喷射出来后会立刻气化（压力降低），气化过程吸热导致温度迅速下降，足以使部分CO2变为CO2(s)。
另一个不同是，CO2固-液的两相平衡线是向右倾斜的，而碘的两相平衡线几乎是一条竖直的直线。线的斜率与熔化过程的体积变化有关，如果熔化过程体积增大，平衡线具有正的斜率(CO2)。反之，其具有负的斜率(H2O)。如果熔化过程体积基本不变，那么平衡线接近直线(I2)。
超临界流体
液体和气体在临界点变得无法区分，这个时候物质可以同时具有液体和气体的某些性质，例如类似液体的高密度，以及类似气体的低粘度以及扩散性。我们用超临界流体(supercritical fluid, SCF)来称呼这种状态。
接近临界点时，压强或者温度的小变化会使密度发生很大变化，因此超临界流体的许多特性可以被『精细调整』。超临界流体常用于工业和实验室过程中的溶剂，而且可以取代许多有毒有害的有机溶剂（如二氯甲烷）。低因咖啡的加工过程涉及超临界二氧化碳对咖啡因的萃取，咖啡豆在约90 °C以及160~220 atm的压力下与二氧化碳SCF接触，使咖啡因含量从正常的1~3%下降到大约0.02%。溶解有咖啡因的二氧化碳SCF降低压力，咖啡因会沉淀出来并被移去，二氧化碳可重复循环使用。
咖啡是世界上流行范围最为广泛的饮料之一，烘焙过的咖啡豆能够以多种方式冲泡为咖啡热饮。/©Negative-Space
水
水的相图是与二氧化碳和碘又有不同。第一是冰I的熔化曲线具有负的斜率，这意味着熔化过程是体积减少的（大多数物质熔化过程体积增加）。第二是固态的冰具有很多不同晶型，最普通的冰被称为冰I，而高压下存在冰II、冰III、冰V、冰VI等不同晶型。
水的部分相图。水的熔化曲线具有负的斜率，此外固态的冰存在多种晶型。
水的部分相图。水的熔化曲线具有负的斜率，此外固态的冰存在多种晶型。
如果我们给一块常压下略低于0°C的冰施加压力——它可能会转化为液态水。这一过程需要的压力非常大，通常是难以观察到的。据称滑冰者冰鞋的冰刀划过冰面的时候，压力会使部分冰熔化，从而减少摩擦力。但这种说法是错误的，因为冰刀施加的压力太小，不足以使表层的冰熔化。合理的解释是，冰块表面的水分子具有与液态水类似的移动方式，因此即使在非常低的温度下，冰面也是『滑』的。
在冰面上溜冰的人，据称滑冰者冰鞋的冰刀划过冰面的时候，压力会使部分冰熔化，从而减少摩擦力。/©Manfred Richter
冰具有多种晶型，普通的冰是冰I，而高压下存在冰II、冰III等不同微观结构的冰。因此冰的三相点除了冰I-液-气(273.16 K, 0.612 kPa)，还具有其他三相点。例如冰I、冰II和冰III的三相点为−34.7 °C，212.9 MPa。另外请注意，除了冰I之外，其他冰的晶型的熔化曲线具有正的斜率。
相与相变
相与物质的状态有什么区别？这两个词具有细微的差别，我们已经知道，物质只有三种状态：固体、液体、气体。而相是具有明确成分和均匀特性的任何物质样本，可与与其接触的其他相区分开来。例如含有水-水蒸气的体系具有两个相，液体是一个相，蒸气是另一个相。在这个情况下，相（液相与气相）与物质的状态（液态和气态）相同。
现在考虑一杯饱和的盐水，杯底有NaCl固体没有溶解。不考虑水蒸气的话，体系有两个相——饱和NaCl溶液、NaCl(s)固相。如果将等体积的水和乙醚混合，液体会分为两层——上层是饱和了水的乙醚溶液，下层是饱和了乙醚的水溶液，它们也是两个相。相图是用来表示相平衡系统的组成与一些参数之间关系的一种图，本章涉及到的相图，其参数是温度和压力。
例题
在−5 °C，101.3 kPa下的一些冰块，在保持温度不变的情况下增加压力，会发生什么变化？请参考水的相图作答。
解答
我们在水的相图−5 °C的位置做一条竖线，很容易看出竖线依次经过如下的区域：冰I、液态水、冰V、冰VI（以及冰VII）。因此随着压力增大，冰I首先熔化为水，然后再次凝固为冰V。冰V在更高的压力下会转变为冰VI或者冰VII。
12.5 固体中的成键
本章剩下的内容会介绍固体物质中的成键，本节会讨论固体中相互作用的类型，包括离子键、共价键、金属键以及范德华力。下一节会讨论微粒在空间中的排布方式。
网络共价固体
在被称为网络共价固体(network covalent solid)的物质中，原子之间以共价键相互连接，共价键遍布整个晶体。共价键是相当强的相互作用，网络共价固体通常具有较高的熔点和硬度。我们考虑碳的两个同素异形体——金刚石和石墨。
金刚石又叫钻石，是一种昂贵的天然宝石，下图展示了金刚石的结构。我们知道碳通常形成4根化学键，金刚石中的碳原子均为$sp^3$杂化，以四面体的形式同周围4个碳原子相连，形成三维网状结构。
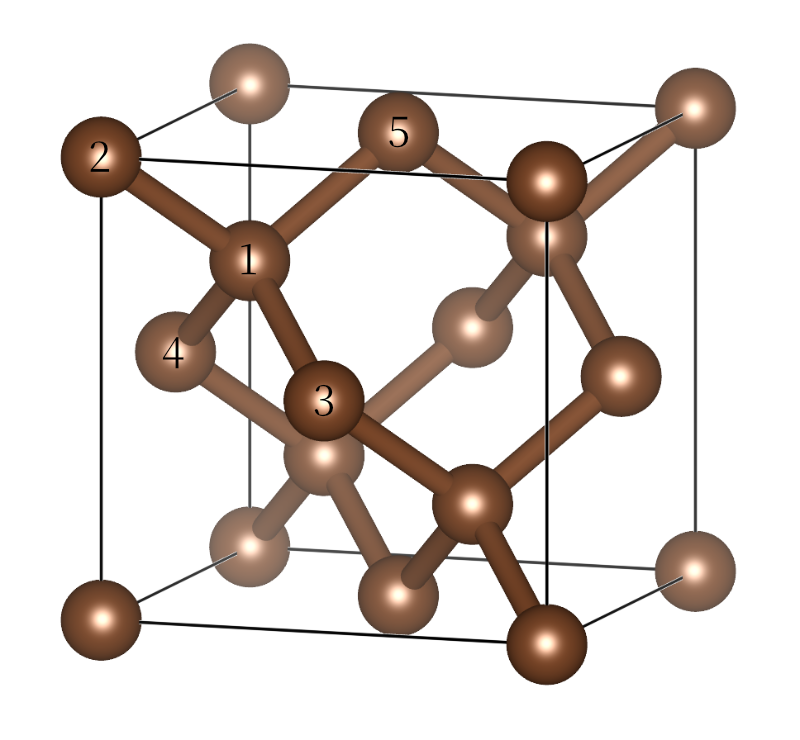金刚石的结构，每个原子以四面体的形式同周围4个碳原子成键，例如1号碳原子与2~5号碳原子成键。
如果金刚石中一半的碳原子被硅取代，就获得了碳化硅的结构。碳化硅又叫金刚砂，其和金刚石都可用于磨料。事实上，金刚石是已知最硬的物质，要划伤金刚石，必须破坏其中的共价键。这两种材料也是非导体，具有很高的熔点或沸点。SiC在2700 °C左右升华，而金刚石在3500 °C以上熔化。
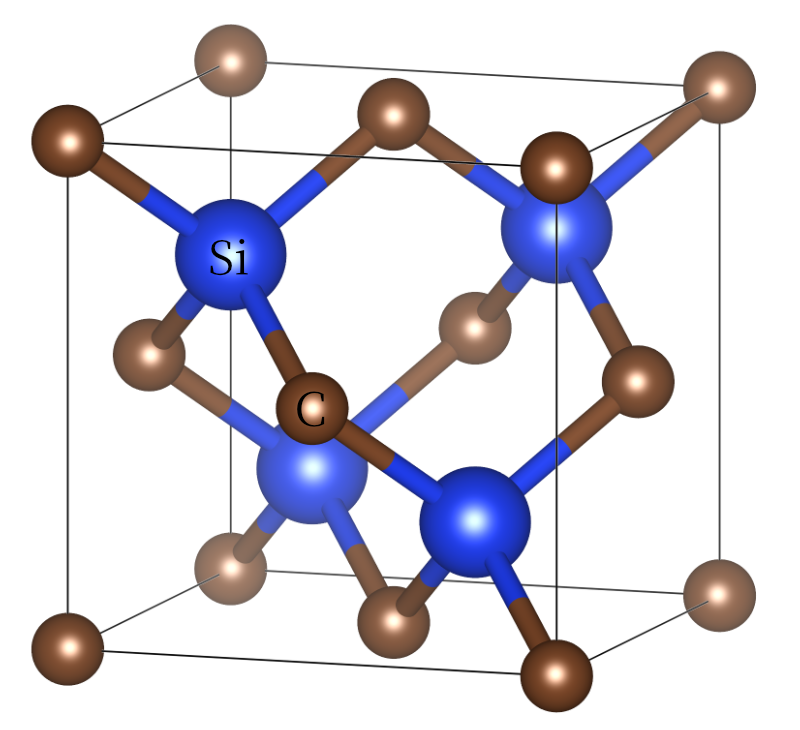碳化硅的结构，其由金刚石的结构变化而来。
石墨是碳的另一种同素异形体，其性质与金刚石截然不同。石墨质软，可以做润滑剂而不是磨料。此外石墨可以导电，而金刚石是不能导电。石墨中的碳是$sp^2$杂化的，每个碳原子与周围三个碳原子以平面三角形的形状成键。没有参与杂化的$p$轨道垂直于层，重叠形成大的离域π体系。层与层之间间距较大，为335 pm，而层内C—C键键长为142 pm。
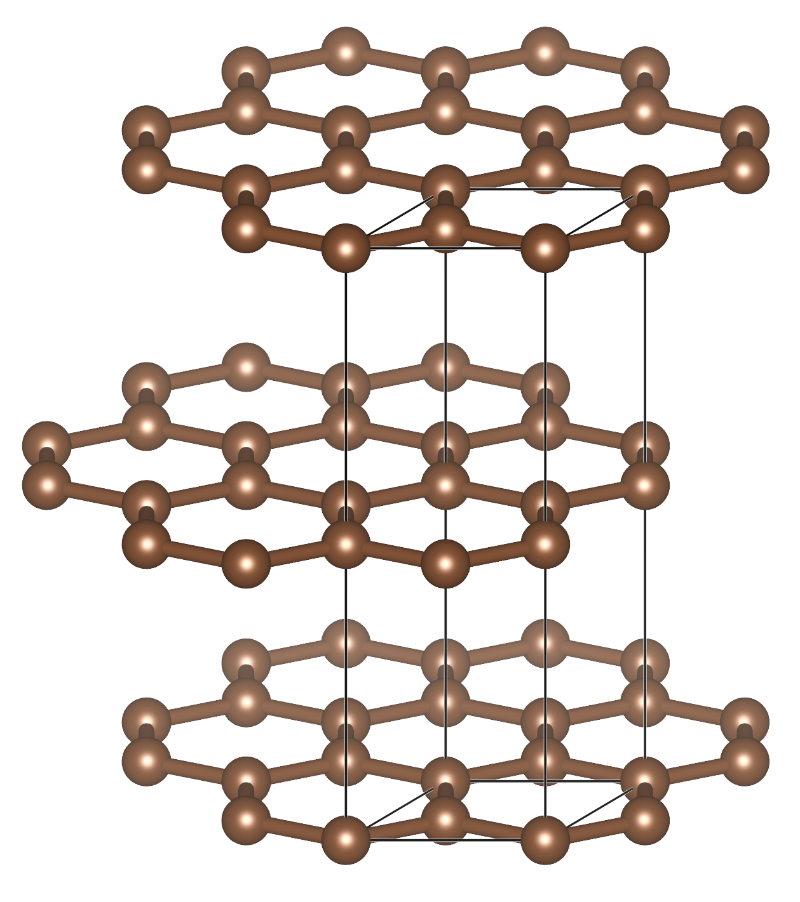石墨的结构，其最显著的特征是层状结构。如果单独抽出一层石墨，就获得了石墨烯。
石墨的层状结构赋予石墨独特的性质，因为层间距离较大，作用力较弱，层与层可以相互滑动，因此石墨可作为润滑剂使用。石墨也可以被剥离成薄片，铅笔的主要成分是石墨，在书写时薄片脱落并粘在纸张上。另外石墨的$p$电子是离域的，在施加电场时电子可沿着碳原子平面移动，因此石墨具有良好的导电性，可用于电解过程中的电极。
碳的其他同素异形体
1985年，在一个模拟红巨星附近环境的实验中，人们发现了很多含碳物质。样品质谱中最强的峰出现在720 u，即对应着C60。在当时为C60提出一个合理的结构是非常具有挑战性的，因为与金刚石或石墨类似的结构都无法解释C60分子。这样的结构中会存在『悬空键』，即达不到碳四价的原子留在结构的边缘。最终人们通过X射线衍射技术证明C60的结构是截角二十面体——一个由12个五边形和20个六边形组成的三维多面体，多面体每个顶点上都有一个碳原子。这样的结构类似于足球，所以人们最早将C60分子称为buckminsterfullerene，即巴克明斯特富勒烯，或口语化表述为buckyball（巴克球）。用来纪念建筑学家巴克明斯特·富勒(Buckminster Fuller)在1967年世界博览会上设计的球形圆顶薄壳建筑。
建筑学家巴克明斯特·富勒设计的美国世界博览馆球形圆顶薄壳建筑。/©pedrik CC BY 2.0
此后人们还发现了许多其他种类的富勒烯，包括C70、C74、C82等。富勒烯也可以形成化合物，例如将一些原子或基团连接在富勒烯表面，或者在富勒烯内部包裹一些原子。现在人们已合成数以千计的富勒烯化合物。
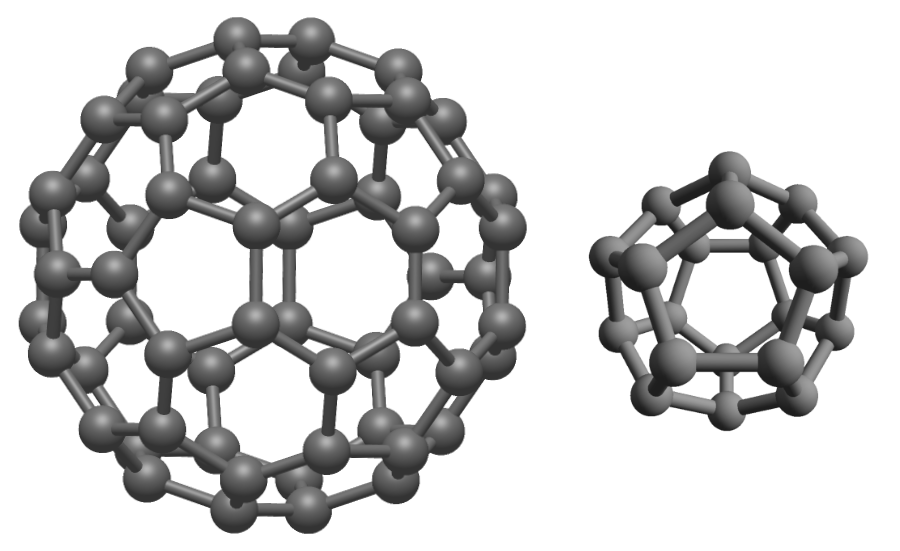C60富勒烯与C20富勒烯。C20富勒烯的结构为五角十二面体，如果我们把五角十二面体的每个顶点都截取一小块，就能获得C60的结构。
在研究富勒烯的过程中，人们发现了另一种碳的同素异形体——碳纳米管。碳纳米管可以看成是卷曲成管状的单层石墨——石墨烯。碳纳米管的直径大约只有几纳米（所以叫做纳米管），而长度可以从数纳米到数微米不等。纳米管具有不寻常的电子和机械性能，例如具有半导体性质的纳米管可用于制造CPU器件。
一种碳纳米管的结构（上）以及碳纳米管的扫描隧道显微图像（下）。/上图 ©Edumol.fi CC BY-SA 2.0 下图 Public Domain
.jpg){kind=link}
离子固体
离子固体(ionic solid)是由阴离子和阳离子组成的固体，你可能好奇离子键的强度到底有多少，它可以通过打碎离子晶体并将阴阳离子分离所需要的能量来度量。晶格能(lattice energy)是将1 mol离子固体转变为气态离子的能量变化（或者说对应量的气态阴阳离子结合生成1 mol离子固体放出的能量）。晶格能可用于预测离子化合物的熔点和水溶性，如果要比较不同化合物晶格能的大小，有如下的两点规则：
离子半径越大，离子之间的吸引力越弱。离子所带电荷数越大，吸引力越强。
对于大多数离子化合物，晶格能足够大，固体很难气化，所以通常温度下离子固体不会升华。如果温度足够高，离子固体会熔化，一般来说晶格能越大，熔点越高。
溶解过程需要克服阴阳离子之间的吸引力，所以通常来说晶格能越大，离子固体越难以溶解。这只是个粗略的想法，因为溶解过程除了能量因素（焓因素）外，还有其他的因素影响，我们会在下一章学习熵。
例题
KI和CaO，何者熔点更高？
解答
K+的半径大于Ca2+，I−半径大于O2−，从离子半径的角度看，KI的晶格能更小。另外CaO的阴阳离子都带两个电荷，所以CaO的熔点更高。
练习
什么物质的熔点应该低于KI？什么物质熔点高于CaO？各举一个例子。
分子固体
分子固体(molecular solid)由分子通过分子间作用力组成。在很低的温度下，稀有气体会通过伦敦力吸引在一起变为固体，所以稀有气体的固体单质是分子固体。
二氧化碳的固体也是分子固体，其结构如下图所示。如果我们把二氧化碳分子抽象看成一个点，二氧化碳分布在立方体晶胞的顶点以及面心。二氧化碳是非极性分子，分子之间仅存在范德华力。
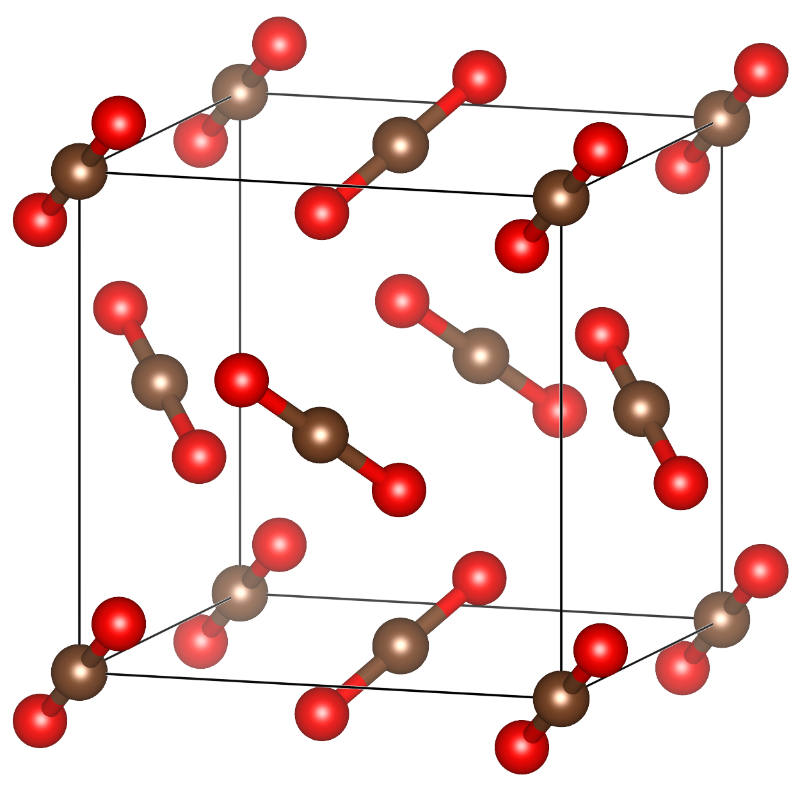二氧化碳的结构，如果我们把二氧化碳抽象成位于碳原子上的一个点，那么二氧化碳分布在立方体晶胞的顶点以及面心。
很多分子固体有类似的结构，只是堆积的方式可能不同。分子固体中涉及的力包括范德华力或者氢键。
金属固体
金属的成键可以看成金属离子浸泡在电子海洋里，因为金属原子的价电子是高度离域的。金属是电的良导体，因为电子可以自由移动。金属键的结合力较强，因此金属固体的熔沸点通常高于分子固体。本节学习的几种固体类型，其中的成键方式总结在下表中。
| 类型 | 微粒 | 微粒间作用力 | 典型性质 | 例子 |
|---|---|---|---|---|
| 金属固体 | 金属离子以及离域电子 | 金属键 | 金属的硬度可软可硬，熔沸点可高可低，取决于具体物质。有光泽、延展性，是热和电的良导体 | Na、Mg、Al、Fe、Sn、Cu、Ag、W |
| 离子固体 | 阴离子与阳离子 | 电磁相互作用（离子键） | 坚硬、易碎。熔点较高，固体的时候不导电，但熔化后可导电。可能溶于极性溶剂，如水中 | NaCl、MgO、NaNO3 |
| 网络共价固体 | 原子 | 共价键 | 坚硬，难以熔化或者升华，通常不导电 | 金刚石、石墨、SiC、AlN、SiO2 |
| 分子固体（非极性） | 原子或非极性分子 | 色散力 | 质软，熔沸点低，溶于非极性溶剂 | He、Ar、H2、O2、CH4、I2 |
| 分子固体（极性） | 极性分子 | 色散力和取向力 | 熔沸点不高，溶于一些非极性溶剂以及极性溶剂 | CHCl3、HCl |
| 分子固体（含氢键） | 含与N、O、F成键H的分子 | 氢键 | 熔沸点不高，溶于一些极性溶剂 | H2O、NH3 |
12.6 晶体结构
晶体是空间形状具有一定规则的固体，其规整的几何外形很早就引起了人们的关注。但对晶体结构的微观认知直到X射线衍射技术发展起来才完善。晶体在微观上具有规则的排布，这些规律会影响物质在宏观上的性质。
晶胞
在讨论三维世界中真实的晶体之前，我们先来想象一下，一维或者二维世界中的晶体长什么样。下图给出了几种一维结构的物质，可以看出这些结构具有重复性。如果我们把最小的重复单元——被称为结构基元——抽象成一个点，称为点阵点，那么一维下的晶体就是由一系列等间隔的点阵点构成：
一些假想的一维晶体，它们的最小重复单元（虚线框），以及抽象成的点阵点。
一些假想的一维晶体，它们的最小重复单元（虚线框），以及抽象成的点阵点。
现在考虑二维周期结构，二维结构的重复单元是平行四边形，下图给出了几种假想二维晶体的结构，以及对应的点阵。任意四个点阵点围成的平行四边形都可以称为晶胞(unit cell)，但一般我们只取对称性较高的平行四边形。例如我们可以从氯化钠的点阵中画出正方形的晶胞，也可以画出一个角度为45°的平行四边形。我们会选对称性更高的正方形作为晶胞。
一些假想的二维晶体，它们的晶胞（虚线框），以及抽象成的点阵点。
一些假想的二维晶体，它们的晶胞（虚线框），以及抽象成的点阵点。
现在考虑三维结构，三维晶体的晶胞形状为平行六面体。奥古斯特·布拉维(Auguste Bravais, 1811-1863)提出三维晶体的点阵排列仅有14种，它们根据平行六面体的参数可分为7个晶系(crystal system)。在普通化学中我们只需掌握其中的两个晶系——立方晶系以及六方晶系。
立方晶系的晶胞为立方体。有三种布拉维格子属于立方晶系，分别为简单立方(cP)、体心立方(cI)以及面心立方(cF)。图中每一个黑点都表示一个点阵点，每个点阵点对应一个结构基元，这三种布拉维格子分别含1、2和4个结构基元。
立方晶系的三种布拉维格子，分别为简单立方、体心立方以及面心立方。
立方晶系的三种布拉维格子，分别为简单立方、体心立方以及面心立方。
那对于体心立方以及面心立方晶胞，我们能否圈出体积更小的平行六面体晶胞呢？答案是肯定的，最小的晶胞被称为素晶胞。我们一般不会对体心立方和面心立方使用素晶胞，因为素晶胞的对称性反而没有现在的好，使用起来并不那么便利。
最密堆积
我们来考虑最简单的晶体结构——仅有一种原子构成的晶体，例如金属晶体。我们把金属原子看成一个个等径圆球，那么最简单的堆积方式就是简单立方堆积。虽然它简单，但采取这种堆积的金属仅有一种，就是钋(Po)。
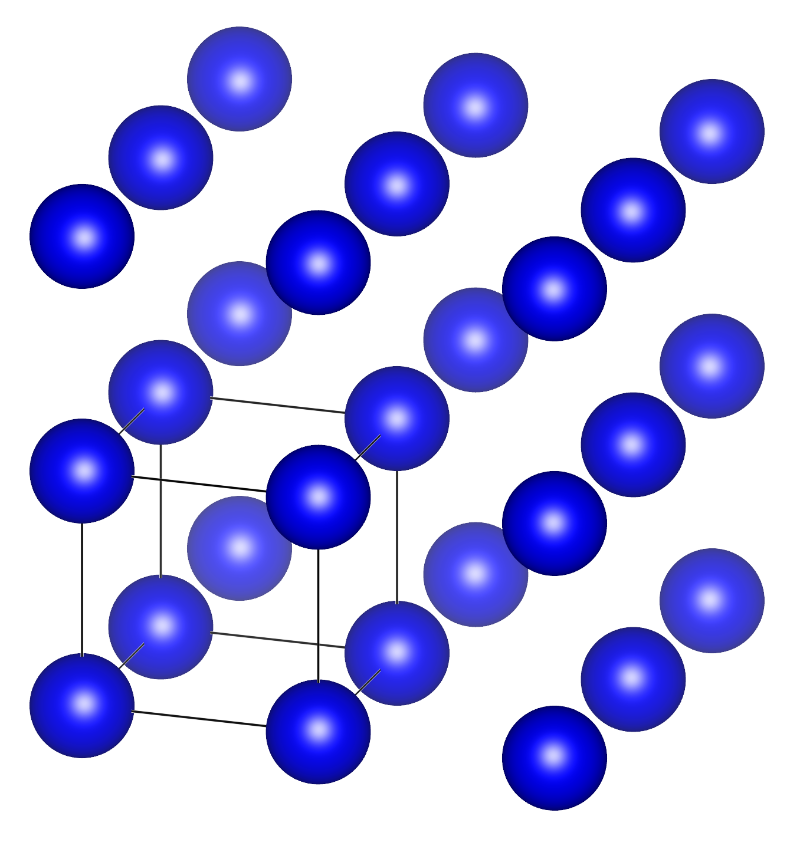钋的简单立方堆积结构，圈出的立方体为晶胞。
这种堆积方式的空间利用率非常低，那么等径圆球如何才能最高效地填满空间呢？我们先来考虑二维中等径圆的排列。要让圆尽可能密地占据二维空间，其排列方式应该为：
二维平面上圆的最密排布方式，每个圆与周围的六个圆相接触。
现在我们把二维圆的密堆积拓展到三维。三维中的球可以采用类似二维密堆的方式形成单原子层，想象一下在桌面上铺上一层弹珠。这样的层我们称为密置单层。我们可以在密置单层的上方再放一层密置单层，使得上层的每个球都放在空隙上方，这样才能更加紧密地堆积。如下图所示，这样的放法有两种：
在密置单层的基础上得到的密置双层有两种堆法。
在密置单层的基础上得到的密置双层有两种堆法。
如果我们在密置双层的基础上继续放密置层，就得到了三维下的最密堆积。这样的堆积方式有无限种，如果我们把灰色原子所在的位置记为A，绿色的记为B，蓝色的记为C。除非相邻两层相同（例如同时出现AA），所得的结构就是最密的。例如ABABABAB⋯是一种最密堆积，ABCABCABC⋯也是一种。这两种最密堆积是最常见的，特别地，我们把第一种称为六方最密堆积(hexagonal closest packed, hcp)，而第二种称为立方最密堆积(cubic closest packed, ccp)。
六方最密堆积结构如下所示，有些学生可能会以为红线圈出的六棱柱是hcp的晶胞，这是错误的。三维晶体的晶胞是平行六面体，所以真正的晶胞是六棱柱的1/3。
以ABA方式堆积的hcp结构，以及其平行六面体晶胞（右图六棱柱的1/3）。
这种形状的晶胞被称为六方晶胞，属于六方晶系。六方晶系的特点是：$a$、$b$边长相等，且夹角为60°，$c$轴与$ab$平面垂直。很多金属单质采用hcp，例如Mg。下图展示了Mg的晶体结构。
Mg的hcp结构，一个晶胞中含两个Mg原子，其中一个位于晶胞的顶点，另一个位于顶部和底部6个Mg原子组成的三棱柱的中心。
Mg的hcp结构，一个晶胞中含两个Mg原子，其中一个位于晶胞的顶点，另一个位于顶部和底部6个Mg原子组成的三棱柱的中心。
镁的一个胞中含两个Mg原子，而不是9个。因为位于平行六面体顶点、面上或者棱上的原子，只有部分处晶胞内，不能按完整的一个算。如果需要计算晶胞内的原子数，请记住一点——晶胞是平移对称的。因此平行六面体某个顶点有原子，剩下的7个顶点也必定存在原子，它们加起来只算一个。类似的，如果在某个棱上有原子，剩下的对应的三条棱上也必定存在原子；如果某个面上有原子，对应的另一个面上也必定存在原子，这样的跨多个晶胞的原子只能被计数一次。
我们可以照猫画虎地画出立方最密堆积(ABCABC⋯)的晶胞，结果是我们又获得了一个六方晶胞。用这个六方晶胞表示立方最密堆积实属有些挂羊头卖狗肉。ccp正确的晶胞如下图中间所示，其具有面心立方(fcc, face centered cubic)的结构，所以ccp和fcc两个词经常表示同一个意思，并且可以混用。尽管这两个图形看起来是如此地不相似，但实际上它们是等同的。立方最密堆积包含三种位置的密置层——A、B、C，我们把不同位置的密置层依次染为橙、红、绿色。
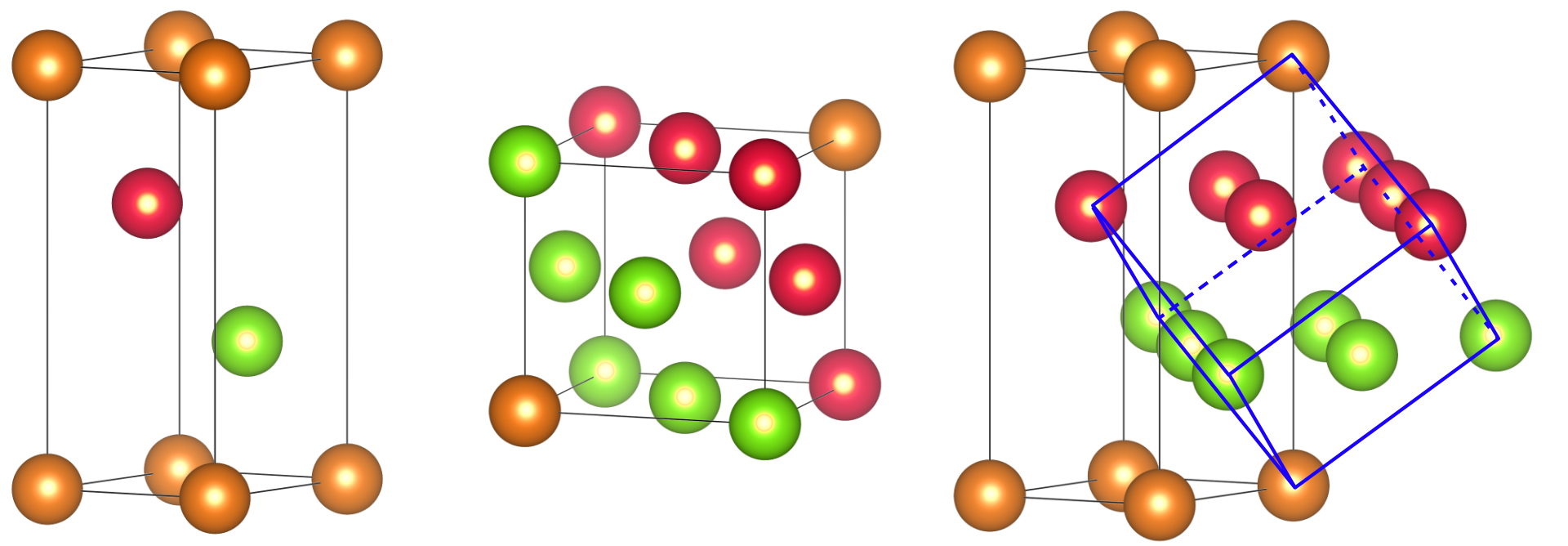左：立方最密堆积的『六方晶胞』，但我们一般不会这么画。中：立方最密堆积常见的表示方式，其具有立方面心的结构。右：这两个结构是等同的，六方晶胞中用蓝线圈出了立方晶胞。
在hcp和ccp结构中，球占据的体积为74.04%。等径圆球的其他任何堆积所占的体积都不可能高于最密堆积。例如体心立方(bcc, body centered cubic)堆积占据68.02%的体积，而简单立方堆积占据的体积更少。
配位数
在金属晶体中，原子和周围的原子可看成是紧密接触的。我们把接触的原子数称为配位数，hcp和ccp的配位数均为12。
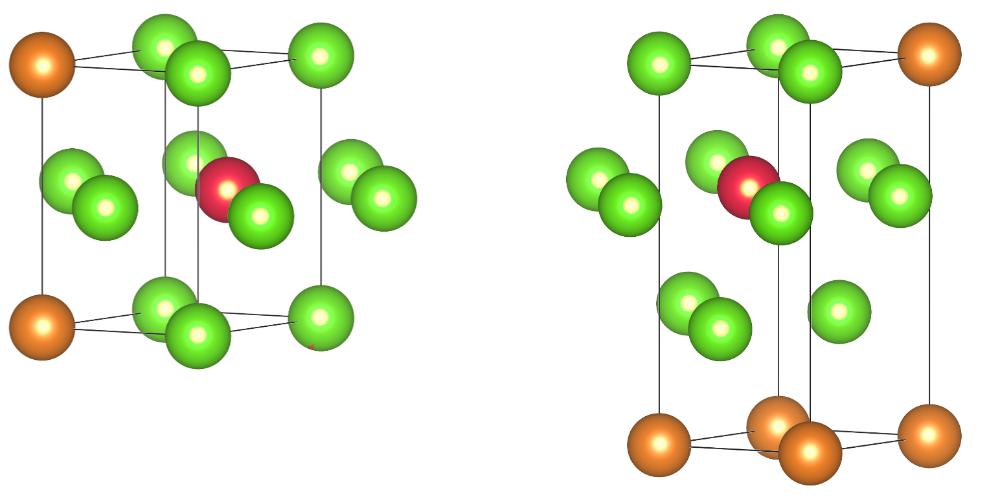观察hcp和ccp结构中染为红色的原子的配位数，同密置单层有6个原子与其接触，底部和顶部各有3个，一共12个。
体心立方堆积的配位数为8，而简单立方堆积的配位数为6。
X射线衍射
我们通过眼睛观察身边的事物，但要观察原子、离子或分子的排布，需要比可见光短得多的光。当一束X射线遇到原子时，X射线与原子中的电子相互作用，使得光向各个方向散射。散射出的X射线相互干涉，最终产生X射线的可见图案，并被检测器探测。通过图案，我们可以推测出晶体中的电子分布，从而确定原子的位置。现代计算机的发展大大加快了X射线图案推导原始结构的过程，过去要获得某晶体的结构数据需数天的人工+计算机计算，而现代电脑只需几秒钟。
下图展示了晶体X射线衍射基本原理，1912年布拉格父子（威廉·亨利·布拉格，William Henry Bragg，1862-1942；威廉·劳伦斯·布拉格，William Lawrence Bragg，1890-1971）提出有关晶体X射线衍射的布拉格定律。特定波长X射线中的两束，标记为a和b，射入晶体，并与晶体中的原子平面呈$\theta$的夹角。a光束被第一层原子平面反射，而b光束被第二层原子平面反射。只有当两束光走过的距离差值刚好是波长$\lambda$的整数倍才会产生相长干涉，使得散射光的强度达到最大。
布拉格衍射定律认为，入射光与晶面的夹角$\theta$、X射线波长$\lambda$以及晶面距$d$之间满足$2d\sin\theta=n\lambda$的关系，才能产生X射线衍射。
布拉格衍射定律认为，入射光与晶面的夹角$\theta$、X射线波长$\lambda$以及晶面距$d$之间满足$2d\sin\theta=n\lambda$的关系，才能产生X射线衍射。
两束光的光程差为$2d\sin\theta$，布拉格定律的公式为：
已知波长的X光以特定角度发生衍射，通过测量角度$\theta$，我们可以计算出晶面距$d$。通过测量晶体在不同方向上的衍射，可以获得晶体中原子位置的信息，即晶体结构。获得了物质的结构，可以计算确定物质的其他性质，例如密度、原子半径。这些计算详见下面的例题。
例题
室温下铁以体心立方堆积，X射线衍射测量表明晶胞边长为287 pm。计算铁的原子半径。
解答
体心立方晶胞，体对角线的长度为4倍半径。因此铁的原子半径为124 pm。
练习
金属铝采用fcc的结构，铝的半径为143.1 pm，那么晶胞的体积为多少pm3？
例题
室温下铁以体心立方堆积，X射线衍射测量表明晶胞边长为287 pm。计算铁的密度。
解答
密度$\rho=\frac{m}{V}$，每个体心立方晶胞含2个Fe原子。密度单位一般取g cm−3，所以质量以g为单位，长度以cm为单位进行计算：$\rho=\frac{55.85\times2}{6.022\times10^{23}}\times\frac{1}{(2.87\times10^{-8})^3}$ = 7.85 g cm−3
练习
金属铝采用fcc的结构，已知铝的密度为2.6984 g cm−3，铝的晶胞边长为404.8 pm，利用这些数据计算$N_\text{A}$的值。
离子晶体结构
很多离子晶体的结构可以看成某种离子（通常是阴离子）以某种方式堆积，而另一种离子填入该种堆积的空隙中。最密堆积有两种类型的空隙，分别为四面体空隙和八面体空隙。顾名思义，四面体空隙是4个原子排列成正四面体的形状后，其内部的空隙。而八面体空隙是6个原子排列成正八面体后内部的空隙。
密置层之间存在四面体空隙（红色三角形）和八面体空隙（红色六边形）。
我们先考虑两层密置层之间的空隙，如果第一层的位置记为A，第二层的位置记为B。那么我们会发现，所有的四面体空隙都与原子重叠，出现在A或者B位上。而八面体空隙出现的位置避开了这两层原子，出现在C位上，即立方最密堆积中的第三层位置。
现在我们来看看hcp结构中两种空隙出现的具体位置。四面体空隙出现在密堆积原子的上方或下方，其数量为密堆积原子的两倍。hcp的晶胞中包含两个原子，以及四个四面体空隙。有两个空隙在$c$轴的棱上，其位于A位原子的上方和下方，用浅红色三角形标记。另外两个四面体空隙在B位原子的上方和下方，用红色三角形标记。
hcp晶胞中四面体空隙以及八面体空隙的位置。
八面体空隙位于C位，其不处于任何原子的正上方或下方，用红色六边形标记。八面体空隙上方有三个最近的原子，且都已在图中绘制出来。下方也有三个最近的原子，只不过只有一个在晶胞内，剩下两个在晶胞外未显示。
ccp晶胞中有四个密堆积的原子，所以有8个四面体空隙以及4个八面体空隙。8个四面体空隙所在的位置刚好组成一个边长为晶胞边长一半的小立方体，且位于晶胞正中心。而八面体空隙位于棱心（三个）以及体心（一个）。
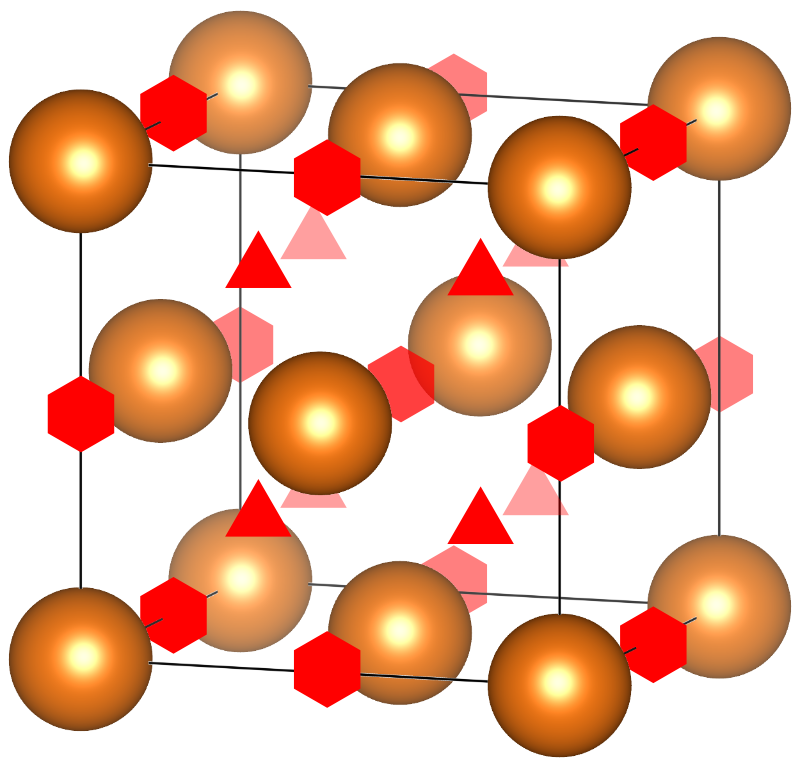ccp晶胞中四面体空隙以及八面体空隙的位置。
这些空隙具体有多大？利用勾股定理很容易算出空隙的大小。如果密堆积的原子半径为$r$，四面体空隙中能够放入最大的球的半径为$r_{\text{t}}$。观察ccp晶胞的某个体对角线，该对角线依次穿过原子、四面体空隙、八面体空隙、四面体空隙、原子。该距离的1/4是四面体空隙中心到原子中心的距离。也就是说$\sqrt{3}a/4=r+r_{\text{t}}$。而$\sqrt{2}a=4r$，所以$r_{\text{t}}=(\sqrt{\frac{3}{2}}-1)r\approx 0.225 r$。
要计算八面体空隙的大小，让我们把关注点转移到晶胞的边。晶胞的每条边都依次穿过原子、八面体空隙、原子，因此有$a/2=r+r_{\text{o}}$。所以$r_{\text{o}}=(\sqrt{2}-1)r\approx 0.414 r$
如果原子不进行密堆积，而是以简单立方的形式堆积。此时的空隙为立方体空隙，立方体空隙的半径为$(\sqrt{3}-1)r\approx 0.732 r$。空隙大小会决定离子化合物的晶体结构。因为阴离子半径通常大于阳离子，我们不妨假设阴离子之间首先相互接触地堆积，而阳离子稍后填入某种空隙。阳离子的半径应该要略大于空隙半径，这样能够挤开相互接触的阴离子，从而减小电荷排斥。所以我们得出了经验上的结论：
- 如果阳离子半径介于阴离子半径的0.225至0.414倍之间，阳离子将填入最密堆积阴离子的四面体空隙中。
- 如果半径介于0.414至0.732倍之间，阳离子将填入最密堆积阴离子的八面体空隙中。
- 如果阳离子半径大于阴离子半径的0.732倍，阴离子将以简单立方堆积，阳离子填入立方体空隙。
这一结论仅考虑了阴离子和阳离子的半径比，忽略了其他因素，因此只能作为经验规则使用。尽管如此，这一结论对于很多物质是有效的，例如氯化钠。Na+的半径为99 pm，而Cl−半径为181 pm，它们比值为0.55，因此我们预计NaCl的结构为：Cl−进行最密堆积，而Na+填充八面体空隙。
Cs+的半径为169 pm，和Cl−相差无几。所以预计CsCl的结构为：Cl−进行简单立方堆积，而Cs+填充立方体空隙。NaCl和CsCl的晶胞如下图所示：
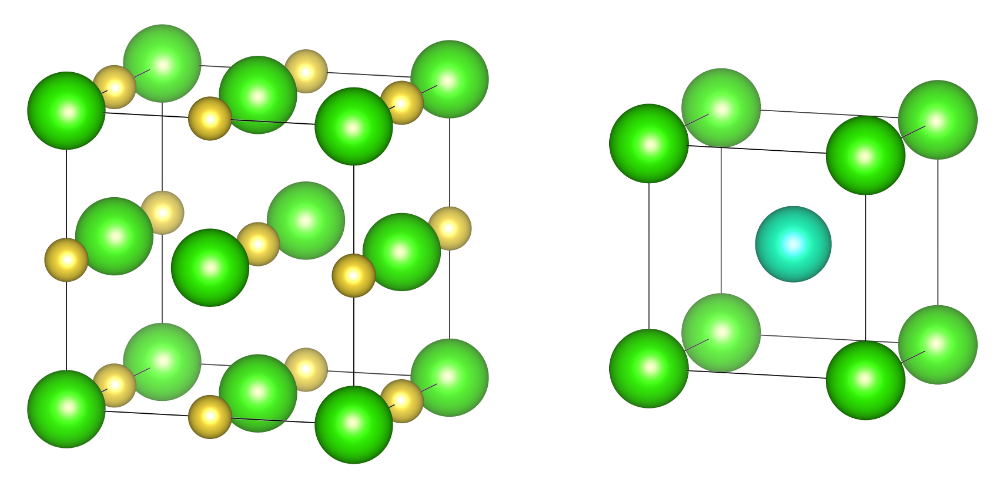NaCl和CsCl的晶胞，Cl占据晶胞顶点。
观察NaCl和CsCl的结构，每个Na周围有6个Cl，而每个Cl的周围有6个Na。事实上Na和Cl的位置完全可以互换，而不影响晶体结构。所以我们也可以这么描述NaCl的结构：Na+进行立方最密堆积，Cl−填充所有的八面体空隙。而Cs周围有8个Cl，比Na要多，这表明原子半径越大，其配位数越大。
很多离子化合物采用NaCl的结构，例如MgO、BaS、CaO。闪锌矿(ZnS)的结构和CaO不同，S以立方最密堆积，而Zn占据一半的四面体空隙；而CaF2的结构中，Ca以立方最密堆积，F占据全部的四面体空隙。它们的晶胞如下所示：
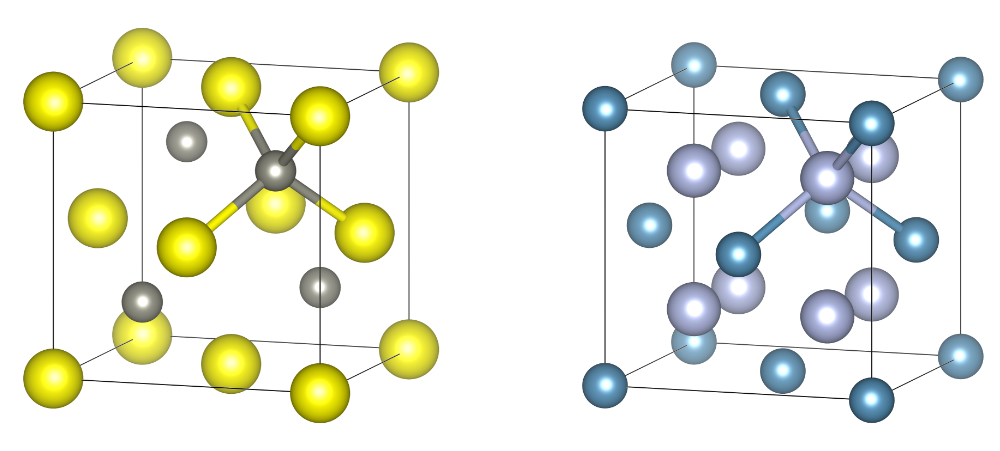ZnS和CaF2的晶胞，占据晶胞顶点的原子分别为S和Ca。
ZnS中Zn和S的配位数均为4，而CaF2中F的配位数为4，Ca的配位数为8。
例题
Na+的半径为99 pm，Cl−半径为181 pm。计算NaCl晶胞的边长$a$。
解答
观察可以发现，晶胞边长等于两倍的Na—Cl距离，即两倍的两者半径之和，为560 pm。
练习
Cs+的半径为169 pm，Cl−半径为181 pm。计算CsCl晶胞的边长$a$。
12.7 离子晶体的晶格能
我们在12.5节介绍的晶格能可以定量描述离子晶体中库仑力的大小，但这一数值很难通过实验直接测定。我们可以通过盖斯定律间接测量晶格能，该方法称为玻恩-哈伯循环，因为由德国科学家马克斯·玻恩和弗里茨·哈伯发明。
以NaCl(s)为例，下图展示了如何间接测量晶格能。
通过玻恩-哈伯循环计算NaCl(s)的晶格能。
通过玻恩-哈伯循环计算NaCl(s)的晶格能。
尽管晶格能我们无法直接测量，但通过NaCl(s)的生成焓$\Delta_{\text{f}}H$、Na(s)的升华焓$\Delta_{\text{sub}}H$、Na原子的电离能$E_i$、Cl2的键焓$E_b$、Cl原子的电子亲合能$EA$，可以构造一个循环计算NaCl(s)的晶格能。现在让我们从Na+(g)+Cl−(g)开始，逆时针走一圈变为NaCl(s)。
- 第一步：Cl−(g)变为Cl(g)，这一步是Cl电子亲合的逆过程，$\Delta H=-EA$ = 349 kJ mol−1。
- 第二步：Cl(g)变为Cl2(g)，焓变数值是氯气键能的一半的相反数，$\Delta H=-0.5E_b$ = −122 kJ mol−1。
- 第三步：Na+(g)变为Na(g)，是Na电离的逆过程，$\Delta H=-E_i$ = −496 kJ mol−1。
- 第四步：Na(g)变为Na(s)，是Na的凝华过程，$\Delta H=-\Delta_{\text{sub}}H$ = −107 kJ mol−1。
- 第五步：Na(s)和Cl2(g)变为NaCl(s)，$\Delta H=\Delta_{\text{f}}H$ = −411 kJ mol−1。
这五步的焓变之和为−787 kJ mol−1，即Na+(g) + Cl−(g) → NaCl(s)的焓变。因此NaCl的晶格能为787 kJ mol−1。
例题
Mg(s)的升华焓为146 kJ mol−1、Cl2(g)键焓为244 kJ mol−1、Mg的第一电离能为738 kJ mol−1、Cl(g)电子亲合能为−349 kJ mol−1、MgCl(s)的晶格能大约为−676 kJ mol−1。请用这些数据计算MgCl(s)的生成焓。
解答
显而易见，$\Delta H$ = 146 + 122 + 738 − 349 − 676 = −19 kJ mol−1。
练习
Cs的升华焓为78.2 kJ mol−1，电离能为376 kJ mol−1，CsCl的生成焓为−442.8 kJ mol−1。不做任何计算，估计CsCl和NaCl的晶格能大小，并通过计算验证。
你可能对例题中MgCl(s)的生成焓为负感到奇怪，这表明MgCl应该是一个稳定的物种，但事实上人们从未获得过MgCl。这并不矛盾，生成焓为负只表明MgCl(s)分解为Mg(s)和Cl2(g)是吸热的，但MgCl可以按照如下方式分解：
MgCl2的晶格能相比MgCl要大很多，因为阳离子电荷数为2。所以MgCl2(s)是很稳定的物质，上面这个反应是强放热的。
那NaCl2是否能够存在？由于Na的第二电离能非常大，所以NaCl2应该不是一个稳定的物种。但在高压下，Na和Cl可以形成比例不为1:1的物质，例如NaCl3、NaCl7。这些物质中Na为+1价，而Cl呈低氧化态。高压下的物质结构同常压下有很大的不同，是现代无机化学家研究的热点方向。