热化学 - 化学课程

封面图：火的使用是人类进化史上的一个里程碑，燃烧释放出的热量可用于烹饪食物。化学反应所伴随的热现象是化学研究的一个重要方面。/©Gábor Adonyi

天然气主要由甲烷组成，碳氢化合物（如甲烷）燃烧的产物是二氧化碳和水。这些反应在生活中非常重要，不是因为产物有用，而是因为反应会放出大量的热。在热水器中燃烧天然气可获得热水，在灶台燃烧天然气以烹饪食物。热化学是与伴随化学反应的热效应有关的化学分支。要了解热与化学和物理变化之间的关系，本章首先从一些基本定义开始。然后我们将了解热量的概念，以及热量在不同体系之间的转移。另一种体系间能量转移的形式是功。结合热和功的概念，我们将学习热力学第一定律的含义，并建立反应热与内能和焓的变化之间的关系。内能变化和焓变的数据可用于直接或间接计算化学和物理变化过程中的能量变化。本章介绍的概念可解释许多实际问题，例如为什么天然气是比煤更好的燃料，为什么脂肪的热量高于碳水化合物和蛋白质的热量。

7.1 入门：一些术语

在本节中，我们将介绍和定义一些非常基本的术语。大多数将在后面的章节中进行更详细的讨论。随着课程的深入，你对这些术语的理解应该会更为深刻。

让我们把宇宙想象成由系统 (system) 及环境组成。系统是我们选择用于研究的宇宙的一部分，它可以和地球上的海洋一样大，也可以像烧杯中的液体一样小。我们研究的大多数系统都很小，我们特别关注系统与其环境之间的能量（如热和功）和物质的传递。环境 (surrounding) 是系统与系统相互作用的宇宙的一部分。下图描绘了三种常见的系统：开放系统 (open system) 与环境自由交换能量和物质。封闭系统 (closed system) 可以与环境交换能量，但不能交换物质。孤立系统 (isolated system) 不与环境相互作用。

thermochemistry-system 三种热化学系统，从左到右依次为孤立系统、封闭系统和开放系统。孤立系统不与环境进行能量、物质交换，如保温杯中的热水。封闭系统能发生能量交换，不发生物质交换，如封闭酒瓶中的香槟。开发系统与环境自由交换能量和物质。/©Aritha ©pasja1000 ©jessicakwok

本节的其余部分以一般的方式更多地说明了能量及其与功的关系。像许多其他科学术语一样，能量 (energy) 源自希腊语 ἐνεργός。它的意思是『在内部工作』。能量是做功 (work) 的能力。当力的作用经过一段距离时，就做了功。移动的物体加速或减速都需要做功。在比萨斜塔上扔下一个铅球，重力对铅球做功。物体因运动而具有的能量称为动能 (kinetic energy)。『动能』源于希腊语 κινέω，意为『使其移动』。通过比较这两个物理量的单位，我们可以看出功和能量之间的关系。一个物体的动能 $E_k$ 取决于它的质量 $m$ 和速度 $u$：$E_k=\frac{1}{2}mu^2$。功 $W$ 则与力（质量 × 加速度）$ma$ 和距离 $d$ 相关：$W=mad$。

当质量、速度、加速度和距离以 SI 单位表示时，动能和功的单位都是 kg m² s⁻²，即 SI 能量单位——焦耳 (J)。1 J = 1 kg m² s⁻²，也就是说：功和能量具有相同的单位。

下图中的弹球蕴含了能量和功的本质。首先将篮球举到起始位置，举起的过程克服重力做功，所做的功作为能量『储存』在球中。这种储存的能量与位置有关，因此被称为势能（potential energy，位能）。

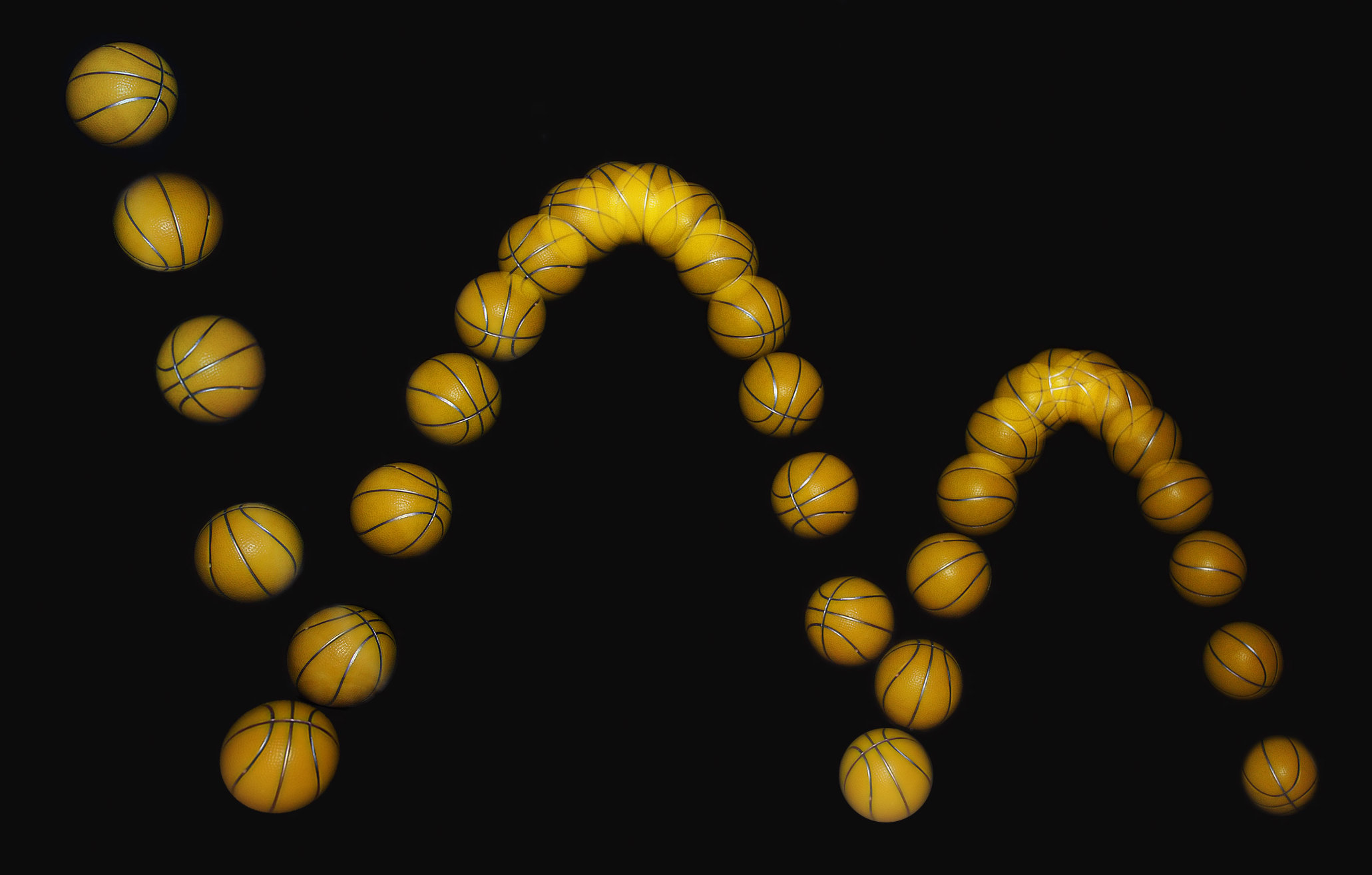bouncing-ball 在 25 Hz 闪光下拍摄的篮球，篮球在高处（左侧）被投下，与地面发生撞击后反弹回来。球与球之间距离越大说明速度越快，动能越大。而球高度越高，所含的势能越大。在撞击地面前的瞬间球具有最大的动能和最低的势能。每一次撞击都会将部分能量转化为热能，因此球的动能和势能之和越来越低。/©MichaelMaggs CC BY-SA 3.0

当我们释放球时，它被重力拉向地球的重心——球落向地面。在下降过程中，势能转化为了动能。当球撞击地面前的瞬间，动能达到最大值。在反弹时，球的动能减少（球减速），势能增加（球上升）。若球与地面的碰撞是完全弹性的，就像分子运动论中分子之间的碰撞一样，球的势能和动能之和将保持不变。球在每次反弹后都会达到相同的最大高度，并永远持续弹跳下去。但现实情况是球很快就会停下来。能量并未凭空消失，势能最终会转化为球、地面和周围空气的原子和分子的额外动能。这种与随机分子运动相关的动能称为热能 (thermal energy)。

一般来说，热能与系统的温度成正比，正如分子运动论所表明的那样（参见 6.7 节）。系统中分子的运动越剧烈，温度越高，其热能也越大。但系统的热能也取决于存在的微粒数量，因此低温下的大样本（如 30 °C 的游泳池）可能比高温下的小样本（如一杯 75 °C 的咖啡）具有更多的热能。因此需严格区分温度和热能。同样重要的，我们也需区分功（力通过距离作用产生的能量变化）和热（涉及热能传递的能量变化）。

7.2 热

热 (heat) 是由于温差在系统与环境之间传递的能量。能量从较热的物体（温度较高）传递到较冷的物体（温度较低），传递的形式是热量。在分子水平上，较热物体的分子通过碰撞失去动能给较冷物体的分子。热能的传递形成『热流』，直到两个物体的平均分子动能变得相同，即温度变得相等。热与功都描述了系统与环境之间传输的能量。

热量传递不仅可以引起温度的变化，在某些情况下还可以改变物质的状态。当固体被加热时，固体的分子、原子或离子的运动更加剧烈，最终克服它们之间的吸引力。在熔化过程中，温度保持恒定，因为外界传递的热能被用来克服固体微粒之间的引力。在恒定温度下发生的过程称为等温过程 (isothermal)。固体完全熔化后，进一步的热流会使液体温度升高。

尽管我们通常使用『放热』、『吸热』、『热流』和『系统向环境散热』等表述，但这并不意味着系统含有热。我们很快会在 7.5 节学习到，系统含有的能量是被称为内能的量。热是系统与环境之间传递的能量。

可以合理推测，改变物质温度所需的热量 $q$ 取决于:

温度变化
物质的量
物质的性质

我们很快就会了解到，实现一定温度变化所需的热量还取决于加热物质的条件（例如物质是在恒容还是恒压条件下加热）。历史上，将 1 kg 水的温度改变 1 °C 所需的热量被称为卡路里 (calorie, cal)。卡路里是一个较小的的单位，千卡 (kcal)是更加常见的单位。热量的 SI 单位是焦耳 (J)，1 cal = 4.184 J。

James-Joule 詹姆斯·焦耳 (James Joule, 1818-1889)，英国物理学家。他在研究热的本质时，发现了热和功之间的转换关系，并由此得到了能量守恒定律，并在最终推导出热力学第一定律。/public domain

本文几乎只使用焦耳表示能量，但一些较早的科学文献中广泛使用卡路里。在生活中卡路里也用于表示食物的能量。

热容

使系统温度改变 1 °C 所需的热量称为系统的热容 (heat capacity)，热容的符号是 $C$。为了测量系统（如反应容器或 10 g 水）的热容，我们对体系提供已知量的热量 $q$，并测量温度变化 $\Delta T$。然后计算热容 $C=\frac{q}{\Delta T}$。

$\Delta T$ 的单位是 °C 或 K，$q$ 的单位是 J，因此热容的单位是 J °C⁻¹ 或 J K⁻¹。这两个单位是可互换的，因为 1 °C 的温度变化和 1 K 的温度变化相同。

若我们知道系统的热容，我们就能将温度变化转换为系统吸收（或放出）的热量（反之亦然）。在下一节我们会了解到，恒压下和恒容下的热容并不相同。为了区分恒压热容和恒容热容，有时会使用符号 $C_p$ 和 $C_V$。我们将考虑的大多数过程发生在恒压下，因此我们通常会使用恒压热容，并经常省略下标 $p$。

对于纯物质，热容通常以每摩尔或每克物质表示。恒压摩尔热容 (molar heat capacity) 符号为 $C_{p,m}$，是在恒压条件下使 1 mol 物质的温度升高 1 °C 所需的热量。恒压比热容 (specific heat capacity) 符号为 $c_p$，有时也称为比热，是在恒压下将 1 g 物质的温度改变 1 °C 所需的热量。在 25 °C 下水的恒压摩尔热容为 75.326 J mol⁻¹ °C⁻¹，而恒压比热容为 4.1813 J g⁻¹ °C⁻¹。

某一纯净物样品的物质的量为 $n$ 或质量为 $m$，样品的恒压热容为 $C=nC_{p,m}=mc_p$。因此有：

$$q=C_p\Delta T=nC_{p,m}\Delta T=mc_p\Delta T$$

例题

将 100.0 mL 水（约 100.0 g）的温度从室温 (21.0 °C) 升高到体温 (37.0 °C) 需多少热量？假设在此温度范围内水的比热容为 4.18 J g⁻¹ °C⁻¹。

解答

代入公式，$q=mc_p\Delta T$ = 100.0 × 4.18 × (37.0 − 21.0) = 6.69×10³ J。

练习

将 2.50 kg 汞的温度从 −20.0 °C 升高到 −6 °C 需提供多少热量？以 kJ 计。已知汞的密度为 13.6 g mL⁻¹，汞的摩尔热容是 28.0 J mol⁻¹ °C⁻¹。

温度变化 $\Delta T=T_\text{f}-T_\text{i}$，其中 $T_\text{f}$ 是最终温度，$T_\text{i}$ 是初始温度。当系统温度升高时，$\Delta T$ 和 $q$ 为正值。$q>0$ 意味着系统吸收（获得）热量。当系统温度降低，$\Delta T$ 和 $q$ 为负值。$q<0$ 意味着系统放出（损失）热量。

计算热量的另一个要点是能量守恒定律 (law of conservation of energy)：在系统与环境之间的相互作用中，总能量保持不变——能量既不产生也不消失。对于热交换，这表明：

$$q_\text{sys}+q_\text{sur}=0$$

其中 $q_\text{sys}$ 是系统的热量变化，$q_\text{sur}$ 是环境的热量变化。因此系统获得的热量来自于环境损失的热量，反之亦然。

$$q_\text{sys}=-q_\text{sur}$$

比热容的实验测定

使用能量守恒定律可以测定物质的比热容。最简单的量热计 (calorimeter) 由一个绝热的容器（如泡沫塑料包裹的烧杯）和温度计组成，容器中装有一定量和温度的水。若要用量热计测量铅的比热容，可以将一定质量较高温度（如 100 °C）的铅粒投入量热计。由于铅粒温度高于水，铅的温度下降而水的温度上升，直到两者温度相同，记录此时的温度。我们可以将铅粒或水视为系统，若铅是系统，因为容器是绝热的，只有水是环境。那么有：$q_\text{lead}=-q_\text{water}$。

例题

量热器中含 50.0 g 22.0 °C 的水，投入 150.0 g 100 °C 的铅粒后，达到平衡时体系温度为 28.8 °C。计算铅的比热容，已知水的比热容为 4.18 J g⁻¹ °C⁻¹。

解答

水温从 22.0 °C 上升 28.8 °C，温度变化为 6.8 °C。铅粒从 100 °C 下降到 28.8 °C，温度变化为 −71.2 °C。$q_\text{water}$ = 50.0 × 6.8 × 4.18 = 1.42×10³ J。故 $c_{p,\text{lead}}$ = − 1.42×10³ ÷ (−71.2) ÷ 150.0 = 0.13 J g⁻¹ °C⁻¹。

练习

量热器中含 50.0 g 26.5 °C 的水，投入 100.0 g 100 °C 的铜后，达到平衡时体系温度为多少？已知水的比热容为 4.18 J g⁻¹ °C⁻¹，铜的比热容为 0.385 J g⁻¹ °C⁻¹。

某些物质的比热容

如前所述，比热容是 1 g 物质温度升高 1 °C 所需要的能量（热量）。当物质被加热时，增加的能量必须被系统的原子、分子或离子吸收。一般来说，1 g 物质中实体的数量越多、这些实体吸收能量的方式越多，比热容的值就越大。

下表列出了一些常见物质的比热容。许多物质比热容小于 1 J g⁻¹ °C⁻¹。但还有些物质，特别是 H₂O(l)，比热容远大于 1 J g⁻¹ °C⁻¹。为什么液态水有很高的比热容？显然水分子的摩尔质量较低，1 g 水中的分子数远大于 1 g 铅中的原子数。因此向 1 g 水和 1 g 铅提供相同的热量，有更多的水分子来分这些能量。因此单个水分子增加的平均能量比单个铅原子要少。在上一章我们已经了解到，温度与系统中粒子平动能有关。但这不是主要原因，主要原因会在第 12 章中学习：水分子之间可以形成氢键。

固体	比热容 (J g⁻¹ °C⁻¹)	液体	比热容 (J g⁻¹ °C⁻¹)	气体	比热容 (J g⁻¹ °C⁻¹)
Pb	0.130	Hg	0.140	CO₂	0.843
Cu	0.385	Br₂	0.474	N₂	1.040
Fe	0.449	CCl₄	0.850	C₃H₈	1.67
S₈	0.708	CH₃COOH	2.14	NH₃	2.06
P₄	0.769	C₂H₅OH	2.44	H₂O	2.08
Al	0.897	H₂O	4.18	H₂	14.3
Mg	1.023
H₂O	2.11

此外热容也与物质状态有关，H₂O(s)、H₂O(l) 和 H₂O(g) 的热容各不相同。固相（冰）中 H₂O 的运动和排列与液相和气相中不同。由于这种差异，固、液和气态具有不同的比热容。

另一个因素是分子结构的复杂性。二氧化碳 CO₂ 和丙烷 C₃H₈ 的摩尔质量均接近 44 g mol⁻¹，但 C₃H₈(g) 的比热容远大于 CO₂(g) 的比热容。因为 C₃H₈ 分子结构比 CO₂ 更复杂，因此 C₃H₈ 分子有更多的方式来吸收所提供的能量。

7.3 反应热和量热计

在第 7.1 节我们了解了热能的概念——与随机分子运动相关的动能。热能是内能的一个组分，内能还包括化学能 (chemical energy)：化学键和分子间吸引力相关的能量。若将化学反应视为一些化学键断裂而另一些化学键形成的过程，那么可以预计系统的化学能会因反应而发生变化。根据能量守恒，一些化学能会转化为其他形式的能量，如热量。反应热 (heat of reaction, $q_\text{rxn}$) 是恒温系统发生化学反应时，系统与其周围环境交换的热量。燃烧反应是非常常见的反应，燃料燃烧的反应热是非常有用的数据。

如果反应发生在孤立系统中，即不周围环境交换物质或能量的系统，反应会导致系统的热能发生变化——温度升高或降低。反应热是当系统恢复到其初始温度时系统与其周围环境之间交换的热量。在测量反应热的实验中，我们通常不会将系统恢复到初始温度，而是计算若恢复至初始温度需交换的热量。为此，系统内放有温度计以记录反应过程中的温度变化，然后利用温度变化和系统的热容来计算恒温下的反应热。

与反应热有关的两个常见术语是放热反应和吸热反应。放热反应 (exothermic reaction) 是在孤立系统导致温度升高或在封闭系统中向周围环境放热的反应。放热反应的反应热为负值。而吸热反应 (endothermic reaction) 会使得孤立系统中的温度降低，或在封闭系统中从环境中获得热量。此时的反应热是正的。反应热是通过实验确定的，量热计是一种用于测量热量的设备。我们会在本节了解两种类型的热量计，它们可近似视为孤立系统。

弹式量热计

下图展示了弹式量热计 (bomb calorimeter) 的结构，它非常适合测量燃烧反应放出的热量。系统是量热计双层外壳内的一切，双层外壳可以有效防止热量传递，可近似认为系统是绝热的。系统包括钢弹及其内容物、钢弹浸入的水、温度计、搅拌器等。钢弹内发生燃烧反应，化学能转化为热能，系统温度升高。反应热 $q_\text{rxn}$ 是系统为恢复到其初始温度而必须损失到周围环境的热量。反过来，该热量等于量热计升高温度所获得的热能的负值 ($-q_\text{cal}$)。

$$q_\text{rxn}=-q_\text{cal}$$ bomb-calorimeter

弹式量热计的钢弹用充满了高压氧气，并用镍丝与燃烧物相连。将组装好的钢弹放入水中，给镍丝通电加热样品发生反应，测量反应完成后的温度变化。由于钢弹的体积固定，反应是在恒容的情况下发生的。 bomb-calorimeter

弹式量热计的钢弹用充满了高压氧气，并用镍丝与燃烧物相连。将组装好的钢弹放入水中，给镍丝通电加热样品发生反应，测量反应完成后的温度变化。由于钢弹的体积固定，反应是在恒容的情况下发生的。

量热计升高（或降低）温度所获得（或失去）的热能可通过温度变化 $\Delta T$ 和量热计的热容 $c_\text{cal}$ 计算：

$$q_\text{cal}=\Delta Tc_\text{cal}$$

因此反应热 $q_\text{rxn}=-\Delta Tc_\text{cal}$。

oxygen-bomb-calorimeter 现代的弹式量热器使用电子温度计，直接通过面板读出数据。右上方的金属物体是被提出装置的钢弹，钢弹内充有高压氧气，并通过镍丝与点火装置相连。/public domain

例题

在弹式量热器中燃烧 1.010 g 蔗糖 C₁₂H₂₂O₁₁，水温从 24.92 °C 升高至 28.33 °C。量热器的热容是 4.90 kJ °C⁻¹。计算蔗糖的摩尔燃烧热，以及食品包装袋上一茶勺蔗糖（约 4.8 g）所应该标注的热量，以 kcal 计。

解答

$q_\text{cal}$ = 4.90 ×10³ × (28.33 − 24.92) = 1.67×10⁴ J。因此每 g 蔗糖的燃烧热为 −16.5 kJ g⁻¹。蔗糖的摩尔质量为 342.3 g mol⁻¹，故蔗糖摩尔燃烧热为 −5.65×10³ kJ mol⁻¹。一茶勺蔗糖含有的热量是 79.2 kJ，即 19 kcal。

练习

苯甲酸 C₆H₅COOH 的燃烧热为 −26.42 kJ g⁻¹。如果 1.176 g 苯甲酸样品在一个弹式量热器中燃烧，使得温度升高 4.96 °C，量热器的热容是多少？

杯式量热计

在普通化学实验室中，杯式量热计 (coffee-cup calorimeter) 比弹式量热计更常见。杯式量热计外部是泡沫聚苯乙烯隔热材料，我们在杯中混合反应物（通常在水溶液中）并测量温度变化。系统是杯子内壁以及内容物，可视为孤立系统。

杯式量热计结构更为简单，反应物通常以溶液的形式加入杯中。 coffee-cup-calorimeter

杯式量热计结构更为简单，反应物通常以溶液的形式加入杯中。

与弹式量热计一样，反应热等于使量热器温度变化的热量的负数。下一个例题是在杯式量热计测量中和反应的热效应，并作了一些假设来简化计算。量热计还有其他的形式，弹式和杯式量热计是最常见的两种。

例题

强酸和强碱的中和反应的离子方程式为：
H⁺(aq) + OH⁻(aq) → H₂O(l)
25.00 mL 2.50 M HCl(aq) 和 25.00 mL 的 2.50 M NaOH(aq)，初始温度均为 21.1 °C，被加入杯式量热计中。搅拌溶液均匀后温度升至 37.8 °C。计算发生 1 mol 中和反应的反应热。

解答

假定溶液体积可直接相加，反应后体积为 50.0 mL。假定 NaCl 稀溶液的密度和比热容均和水相等，$\Delta T$ = 16.7 °C，故 $q_\text{cal}$ = 50.0 × 4.18 × 16.7 = 3.49×10³ J。因此 $q_{\text{rxn,}m}$ = −3.49×10³ ÷ (2.50 × 0.025) = −5.58×10⁴ J mol⁻¹。

练习

初始温度为 24.52 °C 的 100.0 mL 1.020 M HCl 和 50.0 mL 1.988 M NaOH 在杯式量热器中混合，反应完成后混合物的温度是多？

7.4 功

化学反应通常伴随着热效应，而某些反应中还涉及功——即系统对环境做功（或环境对系统做功）。考虑氯酸钾分解成氯化钾和氧气的反应，假定反应是在下图中的奇怪容器中进行的。除了容器圆柱形顶部的活塞可移动，容器其余部分是刚性的。忽略活塞的质量，活塞顶部受到大气压力，而产生的氧气推动活塞向上，这意味着氧气克服大气压力做功。气体膨胀或压缩所涉及的功称为压力-体积功（pressure-volume work，可简称为体积功）。汽车发动机中汽油燃烧形成的气体所做的就是压力-体积功。

容器中发生化学反应：2 KClO₃(s) → 2 KCl(s) + 3 O₂(g)，产生的氧气推动活塞向上对环境做功。 pressure–volume-work

容器中发生化学反应：2 KClO₃(s) → 2 KCl(s) + 3 O₂(g)，产生的氧气推动活塞向上对环境做功。

现在考虑一个更简单的没有化学反应参与的情况，一个顶部开口的圆柱形容器中有一个质轻活塞，将容器分为上下两室。通过容器顶部的开口，可将容器上室抽真空。容器浸入恒温水浴使下室的温度保持恒定。活塞顶部有两个质量为 $M$ 的砝码，若砝码突然被移除了一个，气体会膨胀直到气体体积增加一倍，而气压下降到原本的一半。

在一个假想的装置中，上半部分和下半部分被轻质活塞所分隔。上半部分抽真空而下半部分含有恒定量的恒温气体。活塞上放有两个质量为 $M$ 的砝码。如果一个砝码突然消失，气体会膨胀至体积增加一倍，气体气压变为原来的一半。 pressure–volume-work2

在一个假想的装置中，上半部分和下半部分被轻质活塞所分隔。上半部分抽真空而下半部分含有恒定量的恒温气体。活塞上放有两个质量为 $M$ 的砝码。如果一个砝码突然消失，气体会膨胀至体积增加一倍，气体气压变为原来的一半。

现在考虑如何计算这一过程的体积功。砝码移除一个后顶部只剩一个砝码，气体将剩下的砝码向上移动对外做功，故：$w=-Mg\Delta h$。功是负的，因为作用力（重力）方向和活塞移动方向相反。

假定活塞的面积为 $A$，力除以面积是压力，而高度乘以面积是体积。因此有：

$$w=-\frac{Mg}{A}\Delta hA=-p_\text{ext}\Delta V$$

其中 $p_\text{ext}$ 的压力视为气体的外部压力，在这个思想实验中是由砝码的重量导致的。而高度变化和活塞面积的乘积正好是气体的体积变化，这是气体膨胀所导致的。这一公式有两个地方需要注意，第一是公式带有负号，这是约定的记法。当气体膨胀时，$\Delta V$ 为正，$w$ 为负，表示系统对外做功失去能量。气体被压缩时，$\Delta V$ 为负，$w$ 为正，表示环境对气体做功，系统获得能量。第二是 $p_\text{ext}$ 为外部压力——系统膨胀所抵御的压力或气体压缩所施与的压力。某些情况下系统内压与外压相同，此时公式可直接用 $p$ 表示。

如果压力以 Pa 表示而体积以 m³ 表示，那么功的单位是 Pa m³ 即焦耳。或者压力以 kPa 表示而体积以 L 表示，单位也是 J。使用其他的压力-体积组合所得到的功需正确转化为焦耳。例如 1 bar L = 100 J。

例题

在 298 K 的恒温下，上述容器中有 0.100 mol He，外部压力为 2.40 atm。现在将外部压力减少至 1.20 atm，计算气体膨胀的功，以 J 计。

解答

$w=-p_\text{ext}\Delta V=p_\text{ext}(V_1-V_2)$，$V_1=\frac{nRT}{p_1}$ = 1.02 L，$V_2=\frac{nRT}{p_2}$ = 2.04 L，因此 $w$ = −1.20 × 1.02 × 101.3 = −124 J。

练习

初始温度为 20.0 °C 的 50.0 g N₂，体积为 7.50 L。抵抗 2.50 atm 的外压膨胀，最多可以对外做多少功？

7.5 热力学第一定律

热量的传递和做功会使系统和环境的能量发生变化，系统含有的能量被称为内能，内能 (internal energy, $U$) 是系统的总能量（动能和势能），包括分子的平动能、与分子旋转和振动有关的能量、储存在化学键和分子间吸引力中的化学能，以及亚原子粒子之间的作用能，如电子和原子核相互作用以及原子核内质子和中子的相互作用。我们不能说系统含有热或者功，热 ($q$) 和功 ($w$) 是系统和环境之间能量交换的手段，只有系统发生变化的时候才存在热和功。热和功与系统内能之间的关系用热力学第一定律 (first law of thermodynamics) 描述，即能量守恒定律：

$$\Delta U=q+w$$

热量的吸收或释放以及工作性能需要系统及其周围环境的能量发生变化。在考虑系统的能量时，我们使用内能的概念以及热量和功与它的关系。

孤立系统既不能与周围环境交换热量，也不能做功，所以 $\Delta U_\text{is}=0$，因此：

孤立系统的内能是恒定的。

在使用 $\Delta U=q+w$ 时，有几点需特别注意：

任何进入系统的能量都带有正号。如果系统吸收热量，$q>0$。如果对系统做功，$w>0$。
任何离开系统的能量都带有负号。如果系统放出热量，$q<0$。如果系统做功，$w<0$。
一般来说，系统的内能会因热和功而发生变化。如果进入系统的能量多于离开系统的能量，则 $\Delta U$ 为正。如果离开的能量多于进入的能量，则 $\Delta U$ 为负。
$\Delta U_\text{is}=0$ 意味着 $\Delta U_\text{sys}=-\Delta U_\text{sur}$。也就是说能量是守恒的。

例题

气体在膨胀时吸收了 25 J 的热，并做了 243 J 的功。气体的 $\Delta U$ 是多少？

解答

气体吸热，故 $q$ = 25 J。气体对外做功，故 $w$ = −243 J。因此 $\Delta U$ = −218 J。

练习

系统的内能减少了 125 J，同时系统吸收了 54 J 的热。那么这一过程的功是多少？是谁对谁做功？

状态函数

为了完整地描述一个系统，我们需要指出它的温度、压力以及存在的物质的种类和数量。这些信息确定后，我们就指定了系统的状态。对于系统的特定状态具有唯一值的任何属性都称为状态函数 (state function)。例如 20°C 和 100 kPa 下的纯水样品，其密度为 0.99820 g mL⁻¹。密度是状态函数，对于指定的状态，任何不同的纯水样品的密度都相同。状态函数的值取决于系统的状态，而不是获得该状态的过程。

系统的内能是状态函数，尽管我们无法确定内能的实际值。也就是说，我们不能像描述密度为 0.99820 g mL⁻¹ 那样，写出系统的 $U$ 值。不过我们也不需要知道 $U$ 的实际值。例如如下的过程：将 0 °C 下的 10.0 g 冰（状态 1）加热至 50 °C 的水（状态 2），0°C 下冰的内能为 $U_1$，而 50 ° 下水的内能为 $U_2$。两种状态之间的内能差也是确定的：$\Delta U=U_2-U_1$，这一过程的 $\Delta U$ 是我们可以精确测量的。它是从状态 1 到状态 2 的变化过程中，从周围环境转移到系统的能量。

反过来，将 50 °C 的 10.0 g 水（状态 2）冷却为 0 °C 下的冰（状态 1），这一过程的 $\Delta U’=U_1-U_2=-\Delta U$。连续地看这两个过程，0 °C 下的冰变为 50 °C 的水再变为 0 °C 的冰，总过程中系统内能未发生变化，$\Delta U_\text{tot}=0$，因为内能是状态函数。

路径相关函数

与内能不同，热和功不是状态函数。它们的值取决于系统发生变化时所遵循的路径。298 K 和 2.40 atm 下的 0.100 mol He（状态 1）恒温膨胀至 1.20 atm（状态 2）。我们可以采用两种方案进行，第一个方案一步到位，让状态 1 在 1.20 atm 的外压下膨胀。第二个方案分为两个步骤，首先在 1.80 atm 的外压下膨胀至状态 3，随后在 1.20 atm 的外压下膨胀至状态 2。

在相同的假想装置中，活塞上原本放有四个质量为$M$的砝码。让气体膨胀至体积增加一倍有两种方案：一次性移去两个砝码，或分步移去两个砝码。这两个方案的体积功并不相同，说明功不是状态函数，而是路径相关函数。 two-step-expansion

在相同的假想装置中，活塞上原本放有四个质量为 $M$ 的砝码。让气体膨胀至体积增加一倍有两种方案：一次性移去两个砝码，或分步移去两个砝码。这两个方案的体积功并不相同，说明功不是状态函数，而是路径相关函数。

第一种方案的体积功 $w$ = −124 J（见上一节的例题）。第二种方案的体积功是两个步骤的体积功之和。最初气体的体积为 1.02 L，第一次膨胀后为 1.36 L，第二次膨胀后为 2.04 L。因此总功为 (−1.8 × 0.34 − 1.2 × 0.68) × 101.3 = −144 J。

由于内能是状态的函数，因此两种膨胀过程的 $\Delta U$ 相同（实际上理想气体的等温过程 $\Delta U=0$，即两个过程 $\Delta U$ 均为 0）。但分步膨胀的气体对外做了更多的功。功不是状态函数，它是路径相关函数 (path-dependent function)。在下一节中，我们将了解到热也是路径相关的。

现在考虑第三种方案，最开始的四个砝码用等质量的沙子代替，此时气体处于状态 1 下。如果我们一粒粒地移除一半的沙子——即非常缓慢地降低外压，气体最终也达到状态 2。这种非常缓慢的膨胀以几乎可逆的方式进行，我们也可以从状态 2 一粒粒增加沙子，直到状态 1。从热力学的角度来看，如果系统和环境（以及宇宙）中产生的变化可以通过逆步骤完全消除，那么这个过程是可逆的。可逆过程 (reversible process) 涉及无限多个中间步骤，每个步骤系统变化的幅度极小。移除沙子过程不是完全可逆的，因为沙粒的质量大于无穷小。在这个近似可逆的过程中，存在大量的膨胀步骤。该过程相比让气体直接从状态 1 膨胀到状态 2，对外做了更多的功。

在相同的假想装置中，最初活塞上放有一定质量的沙子，一颗颗地移除沙子直到总质量减少一半。 expansion-sands

在相同的假想装置中，最初活塞上放有一定质量的沙子，一颗颗地移除沙子直到总质量减少一半。

分步膨胀与可逆膨胀之间的真正区别在于，可逆过程中的气体始终与环境保持平衡，而分步过程并非如此。对于涉及有限步骤的过程，系统或环境中产生的变化不能通过逆步骤来完全消除。这样的过程是不可逆的 (irreversible)。在比较一步膨胀和两步膨胀的功时，我们发现两个方案的功并不相同，且两步膨胀对外做了更多的功。实际上，可逆膨胀过程对外做最大可能的功。

7.6 焓

在本节中，我们将热力学第一定律应用于包括化学反应的系统。化学反应可表示为：

$a$ mol A + $b$ mol B + ··· → $c$ mol C + $d$ mol D + ···

大写字母 A、B、C、D 等代表不同的物质。小写字母 $a$、$b$、$c$、$d$ 等，代表平衡方程式中的化学计量系数。对于上述过程，有 $\Delta U=U_f-U_i$。根据热力学第一定律，我们也可以说 $\Delta U=q+w$。如果该过程在弹式量热计中进行，由于反应被限制在钢弹内，体积不变，有 $\Delta V=0$。因此系统不做功，$w=p_\text{ext}\Delta V=0$。若这样的等容过程热为 $q_V$，那么有：

$$\Delta U=q_V$$

可以得出如下结论：对于等容过程（如弹式量热计中的反应），对系统传递的热等于系统的内能变化 $\Delta U$。

但化学反应通常不会在定容下进行，更常见的情况是在烧杯、烧瓶和其他开放容器中发生，并在恒定压力（大气压）下进行。恒压下进行的许多反应中，随着系统的膨胀或收缩（主要是产生气体或气体参与反应），会产生少量的体积功。假定反应在恒压 $p$ 下进行，体积由 $V_\text{i}$ 变为 $V_\text{f}$。那么有 $w=-p_\text{ext}\Delta V$，根据热力学第一定律，有：

$$\Delta U=q_p-p_\text{ext}\Delta V=q_p-p_\text{ext}V_\text{f}+p_\text{ext}V_\text{i}$$

现在用 $U_\text{f}-U_\text{i}$ 代替 $\Delta U$，用 $p_\text{i}V_\text{i}$ 和 $p_\text{f}V_\text{f}$ 代替 $p_\text{ext}V_\text{i}$ 和 $p_\text{ext}V_\text{f}$。那么有：

$$U_\text{f}-U_\text{i}=q_p-p_\text{f}V_\text{f}+p_\text{i}V_\text{i}$$

重新排列：

$$(U_\text{f}+p_\text{f}V_\text{f})-(U_\text{i}+p_\text{i}V_\text{i})=q_p$$

这个表达式的左边是 $U+pV$ 的变化。$U$、$p$、$V$ 都是状态函数，所以 $U+pV$ 也一定是状态函数。该状态函数被定义为焓 (enthalpy, $H$)，是内能与压力体积之积的和：$H=U+pV$。上面的表达式可以写成非常简单的形式，将 $U_\text{f}+p_\text{f}V_\text{f}$ 替换为 $H_\text{f}$，将 $U_\text{i}+p_\text{i}V_\text{i}$ 替换为 $H_\text{i}$，那么有：

$$\Delta H=H_\text{f}-H_\text{i}=q_p$$

也就是说，对于恒温恒压过程(如在开口容器中发生的反应)，系统向环境传递的热等于系统的焓变 $\Delta H$。这一公式是热力学第一定律对恒压过程的陈述。现在进一步考虑 $\Delta H$ 和 $\Delta U$之间的关系。对于恒压过程，有 $q=q_p=\Delta H$ 和 $ w=-p\Delta V$。将其代入 $\Delta U=q+w$，有：

$$\Delta U=\Delta H-p\Delta V$$

该式的最后一项是在恒定外压下与系统体积变化有关的能量（功）。为评估体积功在化学反应中的重要性，考虑以下化学反应：

2 mol CO(g) + 1 mol O₂(g) → 2 mol CO₂(g) U-H-chemical-reaction

在恒温装置中，一氧化碳和氧气发生反应。若活塞被固定，此时发生的是恒温恒容过程。$q_V=\Delta U$ = −563.5 kJ。若活塞不固定，反应后气体分子数减少，体积收缩，环境对系统做功，从而放出更多的热量。$q_p=\Delta H$ = −566.0 kJ。 U-H-chemical-reaction

在恒温装置中，一氧化碳和氧气发生反应。若活塞被固定，此时发生的是恒温恒容过程。$q_V=\Delta U$ = −563.5 kJ。若活塞不固定，反应后气体分子数减少，体积收缩，环境对系统做功，从而放出更多的热量。$q_p=\Delta H$ = −566.0 kJ。

若在 298 K 的恒温条件以及恒压下测量反应生成 2 mol CO₂ 所传递的热量，结果是 −566.0 kJ，说明 566.0 kJ 的能量以热量的形式离系统：$\Delta H$ = −566.0 kJ。反应的体积功是：$p\Delta V=p(V_\text{f}-V_\text{i})$，假定气体是理想的，应用理想气体状态方程，体积功可表示为：

$$p\Delta V=RT(n_\text{f,gas}-n_\text{i,gas})=\Delta n_\text{gas}RT$$

其中 $n_\text{f,gas}$ 是产物 (2 mol CO₂) 中气体的物质的量，$n_\text{i,gas}$ 是反应物 (2 mol CO + 1 mol O₂) 中气体的物质的量。对于上述反应，有：

$p\Delta V$ = 8.314 × 298 × (2 − 3) = −2.5 ×10³ J = 2.5 kJ

内能的变化为：$\Delta U=\Delta H-p\Delta V$ = −566.0 − (−2.5) = −563.5 kJ。

该计算表明，与 $\Delta H$ 相比，$p\Delta V$ 项非常小，所以 $\Delta U$ 和 $\Delta H$ 几乎相同。上述结果可以更一般地表示为：$\Delta H=\Delta U+\Delta n_\text{gas}RT$，或 $q_p=q_V+\Delta n_\text{gas}RT$。

在这些表达式中，$\Delta n$ 是气体物质的量的变化。此外利用这些表达式可推出如下结论：

对于某化学变化，仅当没有净消耗或产生气体时（即 $\Delta n_\text{gas}=0$ 时），恒压下传递的热量 ($q_p$) 才等于在恒容下传递的热量 ($q_V$)。
在298 K 时 $RT$ 大约等于 2.5 kJ mol⁻¹，所以 $q_p$ 和 $q_V$ 之间的区别通常只有数千焦。例如若 $\Delta n_\text{gas}$ = +1 mol 的过程，$q_p-q_V$ 在 298 K 时约为 2.5 kJ。

反应焓

在上一小节，我们了解到 2 mol CO(g) 和 1 mol O₂(g) 在恒温恒压下反应生成 2 mol CO₂(g) 时，系统的焓变为 −566 kJ。我们也可以通过每摩尔反应的焓变来描述这一事实，相应的焓变用 $\Delta_\text{r}H$ 表示，称为反应焓 (enthalpy of reaction)：

2 CO(g) + O₂(g) → 2 CO₂(g) $\Delta_\text{r}H$ = −566 kJ mol⁻¹

这样的方程式被称为热化学反应方程式，注意热化学反应方程式一定要标注物质的状态。

如第四章所述，1 mol 反应是指反应进度等于 1 mol。即 2 mol CO 和 1 mol O₂ 转化为 2 mol CO₂。现在考虑蔗糖燃烧的反应焓：

C₁₂H₂₂O₁₁(s) + 12 O₂(g) → 12 CO₂(g) + 11 H₂O(l) $\Delta_\text{r}H$ = −5.65×10³ kJ mol⁻¹

因此恒温恒压下每摩尔反应的热为 −5.65×10³ kJ。即每 1 mol C₁₂H₂₂O₁₁(s) 与 12 mol O₂(g) 反应生成 12 mol CO₂(g) 和 11 mol H₂O(l)，并放出 5.65×10³ kJ 的热量。有趣的是，该反应的 $n_\text{gas}$ = 0，因此无论反应是在恒压还是恒容下进行，放出的热量都是相同的。

例题

蔗糖燃烧的反应焓是 −5.65×10³ kJ mol⁻¹，1 kg 蔗糖燃烧的热是多少？

解答

蔗糖分子量为 342.3，1 kg 蔗糖含 2.92 mol，完全燃烧的热是 −1.65×10⁴ kJ。负号表示系统放热。

练习

若苯甲酸 C₆H₅COOH 的恒容燃烧热为 −26.42 kJ g⁻¹，计算 1 mol 苯甲酸燃烧反应的焓。

焓变的物理意义

在前面的讨论中，我们使用热力学第一定律 $\Delta U=q+w$ 来证明 $\Delta H=q_p$。$\Delta H=q_p$ 是热力学第一定律的另一种形式，用于恒压过程比较方便。

那么 $\Delta H$ 的物理意义是什么？这个问题的答案非常简单：$\Delta H$ 表示恒压条件下传递的热量。换句话说，我们使用两个不同的符号 $\Delta H$ 和 $q_p$ 来表示同一事物。这些符号中的一个是指系统的属性 ($H$)，另一个是我们可以测量的东西 ($q$)。

属性 $H$ 是否有物理上或分子层面的解释？或许会让你失望，答案是没有。根据定义，$H=U+pV$。$U$、$p$ 和 $V$ 中的每一个都很容易解释。内能 $U$ 代表系统的总能量，它分布在各种分子运动和相互作用中。系统的压力 $p$ 是系统分子在每单位面积上施加的力，而 $V$ 是系统占据的体积。然而，$U+pV$ 的组合没有任何简单的物理意义或分子层面的解释。引入这一组合只是为了方便。如果我们不引入定义 $H=U+pV$，那么恒压热效应就必须用 $\Delta (U+pV)$ 或 $\Delta U+p\Delta V$ 表示。

总之，因为大多数反应是在恒压下进行的，此时测量传递的热量为 $q_p$，这个量也可以表示为 $\Delta H$。

伴随物质状态变化的焓变

当液体与大气接触时，液体表面部分的高动能分子可以克服相邻分子的引力并进入气态。宏观上来说，就是液体蒸发。如果蒸发过程中液体的温度保持恒定，则液体必须从周围吸收热量，以填补蒸发分子带走的能量。蒸发一定量液体所需的热量称为蒸发焓（或气化热）。当蒸发的液体量是 1 mol 时，此时的焓变为摩尔蒸发焓 (molar enthalpy of vaporization, $\Delta_\text{vap}H$)。对于 298.15 K 下的过程：

H₂O(l) → H₂O(g) $\Delta_\text{vap}H$ = 44.0 kJ mol⁻¹

类似的，固体熔化也需要吸收热量，此时的焓变称为熔化焓 (enthalpy of fusion)。在273.15 K 下，对于 1 mol 冰的融化，有：

H₂O(s) → H₂O(l) $\Delta_\text{fus}H$ = 6.01 kJ mol⁻¹

例题

计算将 50.0 g 10 °C 的液态水转化为 25 °C 的水蒸气的 $\Delta H$。

解答

这一过程可分两个步骤进行：将 10 °C 的液态水转化为 25 °C 的液态水，然后再转化为 25 °C 的水蒸气。第一步的 $\Delta H=q_p$ = 50.0 × 4.18 × 15 ÷ 1000 = 3.14 kJ，第二步的 $\Delta H=q_p$ = 50.0 ÷ 18.02 × 44.0 = 122 kJ。因此总 $\Delta H$ = 125 kJ。

练习

若提供的热量为 5.00×10³ kJ，最多可以将多少质量的 −15 °C 的冰转化为 25.0 °C 的水蒸气？已知冰的热容为 2.01 J g⁻¹ °C⁻¹。

标准状态和标准反应焓

反应物和产物的焓与状态有关，因此只有确定了状态，才能确定过程的焓变。如果我们将特定状态定义为反应物和产物的标准状态，那么反应的标准焓变就是反应物和产物处于标准状态的反应中的焓变。标准反应焓 (standard enthalpy of reaction) 用符号 $\Delta_\text{r}H^\ominus$ 表示。

固体或液体物质的标准状态 (standard state) 是在 1 bar 压力和目标温度下的纯单质或化合物。气体的标准状态是在 1 bar 的压力和目标温度下的纯气体，并假定其表现为理想气体。温度不是标准状态定义的一部分，而 $\Delta_\text{r}H^\ominus$ 的数值与温度有关，因此必须标明温度。除非另有说明，本文中给出的值均为 298.15 K 下的。

本章主要使用标准焓变，非标准状态下的焓变会在第 13 章学习。

焓图

若反应的 $\Delta_\text{r}H^\ominus$ 为负的，表示产物的焓低于反应物的焓，反应对外放热，例如蔗糖燃烧反应是放热的。而如下反应：

N₂(g) + O₂(g) → 2 NO(g) $\Delta_\text{r}H^\ominus$ = 180.50 kJ mol⁻¹

产物比反应物具有更高的焓，$\Delta_\text{r}H^\ominus$ 为正。为了增加体系的焓，需要从环境吸收热量。故该反应是吸热的。焓图 (enthalpy diagram) 是过程中焓变化的图形表示。下图展示了如何通过此类图表表示放热和吸热反应。

纵坐标是摩尔焓，横线表示物质焓的大小，越高则 $H$ 越大。当物质从 $H$ 的状态变为$H$低的状态（如水蒸气变为液态水），$\Delta H$ 为负，是放热的。而从焓低低状态变为焓高低状态，该变化的焓变为正，是吸热的。 enthalpy-diagram

纵坐标是摩尔焓，横线表示物质焓的大小，越高则 $H$ 越大。当物质从 $H$ 的状态变为$H$低的状态（如水蒸气变为液态水），$\Delta H$ 为负，是放热的。而从焓低低状态变为焓高低状态，该变化的焓变为正，是吸热的。

7.7 焓变的间接测定：盖斯定律

焓的概念如此有用的原因之一是可以通过少量反应的焓变计算出更多反应的焓变。因为焓变 $\Delta_\text{r}H$ 具有以下性质：

$\Delta_\text{r}H^\ominus$ 取决于反应的书写方式：考虑 25 °C 从元素单质化合形成 NO(g) 的标准焓变：N₂(g) + O₂(g) → 2 NO(g) $\Delta_\text{r}H^\ominus$ = 180.50 kJ mol⁻¹，为了获得生成 1 mol NO(g) 的焓变，我们将所有系数和 $\Delta_\text{r}H$ 的值除以 2：

0.5 N₂(g) + 0.5 O₂(g) → NO(g) $\Delta_\text{r}H^\ominus$ = 90.25 kJ mol⁻¹

逆过程的 $\Delta_\text{r}H^\ominus$ 符号是相反的：由于 $H$ 是状态函数，因此逆过程焓变的符号相反。因此分解 1 mol NO(g)的$\Delta_\text{r}H^\ominus$ 是生成 1 mol NO(g) 的 $-\Delta_\text{r}H^\ominus$。

NO(g) → 0.5 N₂(g) + 0.5 O₂(g) $\Delta_\text{r}H^\ominus$ = −90.25 kJ mol⁻¹

盖斯热总和恒定定律 (Hess′s law of constant heat summation)：反应 N₂(g) 和 O₂(g) 生成 NO₂(g) 的标准焓变：

0.5 N₂(g) + O₂(g) → NO₂(g) $\Delta_\text{r}H^\ominus$ = ?

我们可以认为反应分两步进行：首先 N₂(g) 和 O₂(g) 形成 NO(g)，然后 NO(g) 和 O₂(g) 形成 NO₂(g)。那么有：

0.5 N₂(g) + O₂(g) → NO(g) + 0.5 O₂(g) $\Delta_\text{r}H^\ominus$ = 90.25 kJ mol⁻¹ NO(g) + 0.5 O₂(g) → NO₂(g) $\Delta_\text{r}H^\ominus$ = −57.07 kJ mol⁻¹

0.5 N₂(g) + O₂(g) → NO₂(g) $\Delta_\text{r}H^\ominus$ = 33.18 kJ mol⁻¹

两个方程相加时，NO(g) 出现在方程两侧，从而抵消。我们刚刚介绍了盖斯定律 (Hess′s law)，它阐述了以下原则：

如果一个过程分步进行（即使只是假设），则整个过程的焓变是各个步骤的焓变之和。

因为焓是状态函数，无论从初始状态到最终状态的路径如何，$\Delta_\text{r}H$（或 $\Delta_\text{r}H^\ominus$，若过程在标准条件下进行）具有相同的值。

假设我们想要知道如下反应的标准焓变：

3 C(石墨) + 3 H₂(g) → C₃H₈(g) $\Delta_\text{r}H^\ominus$ = ?

我们应该如何通过实验测量？如果我们试图让石墨和氢发生反应，只会发生轻微的反应，反应并不能完全进行。此外反应产品除了丙烷外还会形成其他的烃。因此不能直接测量反应的 $\Delta_\text{r}H^\ominus$。我们可以通过实验测定其他反应的 $\Delta_\text{r}H^\ominus$，然后进行间接计算。这是盖斯定律最有价值的地方，可以让我们计算无法直接测量的焓变。下一个例题使用标准燃烧焓计算丙烷的生成焓。

例题

C(石墨)、H₂(g) 和 C₃H₈(g) 的标准燃烧焓分别为 −393.5、−285.8、−2219.9 kJ mol⁻¹。计算以下反应的 $\Delta_\text{r}H^\ominus$。
3 C(石墨) + 4 H₂(g) → C₃H₈(g) $\Delta_\text{r}H^\ominus$ = ?
解答

首先写出三种物质的燃烧反应和反应焓，注意标准燃烧焓是 1 mol 物质发生燃烧反应的焓变。
C(石墨) + O₂(g) → CO₂(g) $\Delta_\text{r}H^\ominus_\text{A}$ = −393.5 kJ mol⁻¹ H₂(g) + 0.5 O₂(g) → H₂O(l) $\Delta_\text{r}H^\ominus_\text{b}$ = −285.8 kJ mol⁻¹ C₃H₈(g) + 5 O₂(g) → 3 CO₂(g) + 4 H₂O(l) $\Delta_\text{r}H^\ominus_\text{c}$ = −2219.9 kJ mol⁻¹
上述三个反应分别记为 (a)、(b)、(c)，显而易见，所求反应 = 3 (a) + 4 (b) − (c)，故反应焓 $\Delta_\text{r}H^\ominus=3\Delta_\text{r}H^\ominus_\text{A}+4\Delta_\text{r}H^\ominus_\text{b}-\Delta_\text{r}H^\ominus_\text{c}$ = −104 kJ mol⁻¹。

练习

已知 H₂(g)、CH₃CH=CH₂(g)、CH₃CH₂CH₃(g) 的标准燃烧焓分别为 −285.8、−2057.7、−2219.9 kJ mol⁻¹，计算丙烯加氢反应的 $\Delta_\text{r}H^\ominus$：

H₂(g) + C₃H₆(g) → C₃H₈(g)

7.8 标准生成焓

焓图的纵坐标轴上不会写出任何数值，因为我们无法确定焓 $H$ 的绝对值（因为无法确定 $U$ 的绝对值）。由于焓是状态的函数，因此特定情况下的反应焓变是唯一的。尽管如此，与许多其他属性一样，我们会人为规定一个零点。

考虑三维地图，我们如何确定山的高度？是山顶同地心之间的直线距离吗？还是山顶和海洋中最深的海沟（马里亚纳海沟）之间高度差？实际上山的高度是山顶和平均海平面之间的垂直距离。我们规定指定平均海平面高度为零，地球上的所有其他点都相对于平均海平面的高度就是海拔。最高的山峰，珠穆朗玛峰海拔是 8844 m。而海拔最低的地面是加利福尼亚州死亡谷的 Badwater，为 −86 m。我们也可以对焓进行类似的处理，以元素单质的某些形式的焓作为零点，并依此确定其他物质相对于零点的焓。

物质的标准生成焓 (standard enthalpy of formation, $\Delta_\text{f}H^\ominus$) 是从标准状态的元素的参考形态生成 1 mol 标准状态的物质的焓变。除了少数情况外，元素的参考形态是在 1 bar 的压力和指定温度下元素的最稳定形态。$\ominus$ 符号表示焓变是标准焓变，下标 $\text{f}$ 表示反应是物质由其元素生成的反应。显然：

参考形态的元素单质的标准生成焓为0。

下方给出了几种元素在 298.15 K 下的参考形态。

Na(s) H₂(g) N₂(g) O₂(g) C(石墨) Br₂(l)

有些元素存在同素异形体，例如碳。除了石墨之外，碳的单质还包括金刚石。这两个物质的焓存在明显的差异，因此不能将两种物质的 $\Delta_\text{f}H^\ominus$ 都指定为 0。

C(石墨) → C(金刚石) $\Delta_\text{r}H^\ominus$ = 1.9 kJ mol⁻¹

我们选择更稳定的形态作为参考形态，即具有较低焓的形态。因此我们规定指定 $\Delta_\text{f}H^\ominus$(石墨) = 0，$\Delta_\text{f}H^\ominus$(金刚石) = 1.9 kJ mol⁻¹。

尽管我们可以在 298.15 K 下获得溴蒸汽或液溴，但 Br₂(l) 是最稳定的形式。如果在 298.15 K 和 1 bar 下获得 Br₂(g)，它会立即冷凝为 Br₂(l)：

Br₂(g) → Br₂(l) $\Delta_\text{r}H^\ominus$ = −30.91 kJ mol⁻¹

因此 $\Delta_\text{f}H^\ominus$Br₂(l) = 0，$\Delta_\text{f}H^\ominus$Br₂(g) = 30.91 kJ mol⁻¹。

参考形态不是最稳定形式的罕见情况是磷元素。尽管随着时间的推移白磷会转化为红磷，但仍选择白磷作为参考形态。

P(s,white) → P(s,red) $\Delta_\text{r}H^\ominus$ = −17.6 kJ mol⁻¹

因此白磷的生成焓 $\Delta_\text{f}H^\ominus$P(s,white) = 0，$\Delta_\text{f}H^\ominus$P(s,red) = −17.6 kJ mol⁻¹。

white-and-red-phosphorus 白磷（左）与红磷（右）都是磷的单质。白磷也叫黄磷，呈黄色是因为杂质的存在。白磷长时间放置后，会逐渐转化为红磷，光照会加速这一过程。/©Jumk.de CC BY 3.0

下表列出了一些常见物质的标准生成焓。标准生成焓可能是正也可能是负的，且标准生成焓与物质状态有关。我们将在各种计算中使用标准生成焓。要注意如何书写 $\Delta_\text{f}H^\ominus$ 对应的化学方程式。

物质	$\Delta_\text{f}H^\ominus$/kJ mol⁻¹	物质	$\Delta_\text{f}H^\ominus$/kJ mol⁻¹
CO(g)	−110.5	HBr(g)	−36.40
CO₂(g)	−393.5	HI(g)	26.48
CH₄(g)	−74.81	H₂O(g)	−241.8
C₂H₂(g)	226.7	H₂O(l)	−285.8
C₂H₄(g)	52.26	H₂S(g)	−20.63
C₂H₆(g)	−84.68	NH₃(g)	−46.11
C₃H₈(g)	−103.8	NO(g)	90.25
C₄H₁₀(g)	−125.6	N₂O(g)	82.05
CH₃OH(l)	−238.7	NO₂(g)	33.18
C₂H₅OH(l)	−277.7	N₂O₄(g)	9.16
HF(g)	−271.1	SO₂(g)	−296.8
HCl(g)	−92.31	SO₃(g)	−395.7

例题

甲醛的标准生成焓 $\Delta_\text{f}H^\ominus$ = −108.6 kJ mol⁻¹。写出该焓变对应的热化学反应方程式。

解答

甲醛化学式为 HCHO，在常温下为气体。所以：
H₂(g) + 0.5 O₂(g) + C(石墨) → HCHO(g) $\Delta_\text{r}H^\ominus$ = −108.6 kJ mol⁻¹
练习

亮氨酸 C₆H₁₃O₂N(s) 的生成焓为 −637.3 kJ mol⁻¹，写出该焓变对应的热化学反应方程式。

标准反应焓

如果反应物和反应产物处于标准状态，那么焓变就是标准反应焓 $\Delta_\text{r}H^\ominus$，标准生成焓的主要用途之一是计算标准反应焓。

让我们使用盖斯定律来计算碳酸氢钠分解的标准反应焓，这是在烘焙中使用小苏打时发生的次要反应。

2 NaHCO₃(s) → Na₂CO₃(s) + H₂O(l) + CO₂(g) $\Delta_\text{r}H^\ominus$ = ?

根据盖斯定律，如下的四个方程相加可得到上述方程。

2 NaHCO₃(s) → 2 Na(s) + H₂(g) + 2 C(石墨) + 3 O₂(g) $\Delta_\text{r}H^\ominus=-2\Delta_\text{f}H^\ominus_a$ 2 Na(s) + C(石墨) + 1.5 O₂(g) → Na₂CO₃(s) $\Delta_\text{r}H^\ominus=\Delta_\text{f}H^\ominus_b$ H₂(g) + 0.5 O₂(g) → H₂O(l) $\Delta_\text{r}H^\ominus=\Delta_\text{f}H^\ominus_c$ C(石墨) + O₂(g) → CO₂(g) $\Delta_\text{r}H^\ominus=\Delta_\text{f}H^\ominus_d$

其中 $\Delta_\text{f}H^\ominus$ 下标的 $abcd$ 分别表示 NaHCO₃(s)、Na₂CO₃(s)、H₂O(l)、CO₂(g) 的生成焓。

因此分解反应的 $\Delta_\text{r}H^\ominus$ 可表示为：

$$\Delta_\text{r}H^\ominus=-2\Delta_\text{f}H^\ominus_a+\Delta_\text{f}H^\ominus_b+\Delta_\text{f}H^\ominus_c+\Delta_\text{f}H^\ominus_d$$

由此我们可以得到更普遍的结论，对于反应：

$a$ A + $b$ B + ··· → $c$ C + $d$ D + ···

大写字母 A、B、C、D 等代表不同的物质。小写字母 $a$、$b$、$c$、$d$ 等，代表平衡方程式中的化学计量系数。反应的 $\Delta_\text{r}H^\ominus$ 可表示为：

$$\Delta_\text{r}H^\ominus=(c\Delta_\text{f}H^\ominus_\text{c}+d\Delta_\text{f}H^\ominus_\text{D}+\cdots)-(a\Delta_\text{f}H^\ominus_\text{A}+b\Delta_\text{f}H^\ominus_\text{b}+\cdots)$$

系数 $a$、$b$、$c$、$d$ 等也可用第四章学过的化学计量数 ($\nu$) 表示，即：

$$ \begin{align} \Delta_\text{r}H^\ominus&=\nu_\text{A}\Delta_\text{f}H^\ominus_\text{A}+\nu_\text{b}\Delta_\text{f}H^\ominus_\text{b}+\nu_\text{c}\Delta_\text{f}H^\ominus_\text{c}+\nu_\text{D}\Delta_\text{f}H^\ominus_\text{D}+\cdots\\ &=\sum\nu_i\Delta_\text{f}H^\ominus_i \end{align} $$

例题

计算乙烷燃烧的反应焓。

解答

乙烷燃烧反应方程式为：
C₂H₆(g) + 3.5 O₂(g) → 2 CO₂(g) + 3 H₂O(l)
因此反应的 $\Delta_\text{r}H^\ominus$ = 2 $\Delta_\text{f}H^\ominus$CO₂(g) + 3 $\Delta_\text{f}H^\ominus$H₂O(l) − $\Delta_\text{f}H^\ominus$C₂H₆(g) = −1559.7 kJ mol⁻¹。

练习

计算液态乙醇在 298.15 K 下的燃烧热。

例题

利用如下数据和本章提到的生成焓表计算液态苯的生成焓。
2 C₆H₆(l) + 15 O₂(g) → 12 CO₂(g) + 6 H₂O(l) $\Delta_\text{r}H^\ominus$ = −6535 kJ mol⁻¹
解答

反应的 $\Delta_\text{r}H^\ominus$ = 12 $\Delta_\text{f}H^\ominus$CO₂(g) + 6 $\Delta_\text{f}H^\ominus$H₂O(l) − 2 $\Delta_\text{f}H^\ominus$C₆H₆(l) = −6535 kJ mol⁻¹，代入数据求得 $\Delta_\text{f}H^\ominus$C₆H₆(l) = 49 kJ mol⁻¹。

练习

二甲醚 (CH₃)₂O 的标准燃烧焓是 −31.70 kJ g⁻¹，利用本章提到的生成焓表计算两分子甲醇脱水得到二甲醚的反应焓：

2 CH₃OH(l) → (CH₃)₂O(g) + H₂O(l) $\Delta_\text{r}H^\ominus$ = ?

溶液中涉及离子的反应

水溶液中的许多化学反应最好看作是离子之间的反应，并用离子反应方程式来表示。例如用强碱中和强酸，我们在例题中计算过该反应的中和焓：

H⁺(aq) + OH⁻(aq) → H₂O(l) $\Delta_\text{r}H^\ominus$ = −55.8 kJ mol⁻¹

我们已经知道了 H₂O(l) 的生成焓，如果我们知道任何一个离子的生成焓就可以获得另一个离子的。化学反应不会产生单一类型的离子，总是同时产生阳离子和阴离子，就像钠和氯反应生成 Na⁺ 和 Cl⁻ 一样。所以人们规定 H⁺在水溶液中的生成焓为零。其他离子的生成焓与该参考离子进行比较就能获得数据，例如可以计算 OH⁻(aq) 的生成焓：

$\Delta_\text{f}H^\ominus$OH⁻(aq) = −230.0 kJ mol⁻¹

下表列出了水溶液中几种常见离子的数据。溶液中离子的生成焓和溶质浓度有关，下表中的数据是浓度约 1 M 的水溶液的。

离子	$\Delta_\text{f}H^\ominus$/kJ mol⁻¹	离子	$\Delta_\text{f}H^\ominus$/kJ mol⁻¹
H⁺	0	OH⁻	−230.0
Li⁺	−278.5	Cl⁻	−167.2
Na⁺	−240.1	Br⁻	−121.6
K⁺	−252.4	I⁻	−55.19
NH₄⁺	−132.5	NO₃⁻	−205.0
Ag⁺	105.6	CO₃²⁻	−677.1
Mg²⁺	−466.9	S²⁻	33.05
Ca²⁺	−542.8	SO₄²⁻	−909.3
Ba²⁺	−537.6	S₂O₃²⁻	−648.5
Cu²⁺	64.77	PO₄³⁻	−1277
Al³⁺	−531

例题

已知硫酸钡的生成焓 $\Delta_\text{f}H^\ominus$ = −1473 kJ mol⁻¹。硫酸钡沉淀反应的焓变是多少？

解答

沉淀反应方程式为：
Ba²⁺(aq) + SO₄²⁻(aq) → BaSO₄(s)
反应的 $\Delta_\text{r}H^\ominus$ = $\Delta_\text{f}H^\ominus$BaSO₄(s) − $\Delta_\text{f}H^\ominus$Ba²⁺(aq) − $\Delta_\text{f}H^\ominus$SO₄²⁻(aq) = −26 kJ mol⁻¹。

练习

已知 Ag₂CO₃ 沉淀的反应焓为 −39.9 kJ mol⁻¹，计算 Ag₂CO₃ 的生成焓。

7.9 能源与燃料

热化学测量和计算的最重要用途之一是评估作为能源的材料。在大多数情况下，这些称为燃料的材料通过燃烧反应释放热量。我们将简要了解一些常见的燃料，作为热化学章节的收尾。

化石燃料

当前的大部分能源需求由石油、天然气和煤炭（即所谓的化石燃料）满足。这些燃料来源于数亿年前的植物和动物。这些燃料中的能量的来源于太阳能的固定。在光合作用中，CO₂ 和 H₂O 在酶、叶绿素和光的作用下转化为碳水化合物。即化学式为 C_m(H₂O)_n 的化合物，其中 $m$ 和 $n$ 是正整数。葡萄糖就是一种碳水化合物，其中 $m=n=6$，即 C₆H₁₂O₆。通过光合作用生成葡萄糖是吸热过程，表示为：

6 CO₂(g) + 6 H₂O(l) → C₆H₁₂O₆(s) + 6 O₂(g) $\Delta_\text{r}H^\ominus$ = +2.8×10³ kJ mol⁻¹

上述反应的逆反应就是葡萄糖的燃烧，燃烧反应是放热的。

另一种碳水化合物，纤维素是植物的主要结构材料，分子量高达 500,000 u。当植物在细菌的存在下分解并与空气接触时，O 和 H 会被被去除，残留物的碳含量逐渐增加:

泥炭 → 褐煤(32% C) → 烟煤(60% C) → 无烟煤(80% C)

这个过程大约需要大约 3 亿年的时间才能获得无烟煤。煤是一种可燃的有机岩石，由碳、氢和氧以及少量的氮、硫和矿物质（灰分）组成。（烟煤『分子』的一个提议公式是 C₁₅₃H₁₁₅N₃O₁₃S₂。）

石油和天然气以不同的方式形成。生活在古代海洋中的动植物遗骸落入海底，在那里被细菌分解并被沙子和泥土覆盖。随着时间的推移，沙子和泥土因埋藏在底下而转化为砂岩。上覆砂岩岩层产生的高压和高温将原始有机物转化为石油和天然气。石油矿床的年龄从大约 2.5 亿年到 5 亿年不等。

典型的天然气由大约 85% 的甲烷、10% 的乙烷、3% 的丙烷和少量其他可燃气体和不可燃气体组成。典型的石油由数百种不同的碳氢化合物组成，其复杂程度从简单的甲烷到 C₄₀H₈₂ 甚至更多的碳。

比较不同燃料的一种方法是通过它们的燃烧热：通常燃烧热越高，燃料越好。下表列出了一些燃料的近似燃烧热。这些数据表明，生物质（生物或由其衍生的材料——木材、酒精、城市垃圾）是一种可行的燃料，但化石燃料每单位质量产生更多的能量。

燃料	燃烧热/kJ g⁻¹	燃料	燃烧热/kJ g⁻¹
可燃垃圾	−12.7	烟煤	−28.3
纤维素	−17.5	异辛烷（汽油成分）	−47.8
松木	−21.2	天然气	−49.5
泥炭	−20.8

化石燃料使用带来的问题：化石燃料的使用存在两个基本问题。首先，化石燃料本质上是不可再生能源。在可预见的未来，世界化石燃料的消费量预计会增加，但地球上这些燃料的供应迟早会耗尽。化石燃料的第二个问题是它们对环境的影响。燃料中的硫杂质会产生硫氧化物。与燃烧相关的高温导致空气中的 N₂ 和 O₂ 反应形成氮氧化物。硫和氮的氧化物与空气污染有关，并且是导致酸雨等环境问题的重要因素。化石燃料燃烧的另一个不可避免的产物是二氧化碳，它是导致全球变暖和地球气候潜在变化的『温室』气体之一。

全球变暖——涉及二氧化碳的环境问题：我们通常不认为二氧化碳是空气污染物，因为它本质上是无毒的，且是空气的一种天然和必要成分。然而它对环境的最终影响可能非常显著。大气中 CO₂ 的累积可能会扰乱地球上的能量平衡。

来自太阳的可见光和紫外线辐射在很大程度上对大气是透明的。这种辐射在地球表面被吸收，导致地面温度升高加热。一些吸收的能量被重新以红外线对形式对外辐射。某些大气气体，主要是二氧化碳、甲烷和水蒸气，会吸收一些红外线辐射，使得更多的能量被地球吸收。这一过程通常被比作温室中热能的保留，称为『温室效应』。自然温室效应对于维持地球上生命的适宜温度至关重要，不然地球将永远被冰覆盖。

在过去的 40 万年中，大气中的二氧化碳浓度从 180 ppm 到 300 ppm 不等，工业时代前的浓度约为 285 ppm。到 2021 年，二氧化碳水平已上升至约 416 ppm，且仍在上升。燃烧含碳燃料（如木材、煤、天然气和汽油）以及热带地区的森林砍伐（植物通过光合作用消耗大气中的二氧化碳）会导致大气中二氧化碳浓度增加。二氧化碳积聚的预期影响是地球平均温度升高，即全球变暖 (global warming)。科学家估计，到本世纪末之前，二氧化碳浓度可能会比工业化前时期增加一倍，并导致全球平均温度升高 1.5 至 4.5 °C。

预测大气中 CO₂ 累积的可能影响主要是通过计算机模型完成的，很难知道这些模型中应包含的所有因素以及这些因素的相对重要性。例如，全球变暖可能导致水蒸发增加和云形成增加。反过来，增加的云层可以减少到达地球表面的太阳辐射量，并在一定程度上抵消全球变暖。

全球变暖的一些重要可能影响是：

局部温度变化。在过去的 50 年中，北京平均气温上升了约 2.3°C，而广州平均气温升高约 1.3 °C。
海水热膨胀和大陆冰盖融化加剧导致海平面上升。到 2100 年，海平面可能上升 1 m，仅孟加拉国就有数千万居民流离失所。
植物和动物物种的迁移。现在全球某些地区特有的植被可能会迁移到距两极更近数百公里的地区。疟疾等疾病流行的地区也可能扩大。

尽管目前的一些想法涉及推测，但越来越多的证据支持全球变暖的可能性，这对气候变化有重大影响。例如，对南极冰盖中的微小气泡的分析表明，过去 16 万年大气 CO₂ 浓度与温度之间存在很强的相关性——CO₂ 含量低时的低温和 CO₂ 含量较高时的高温。

CO₂ 不是唯一的温室气体。有几种气体是更强的红外线吸收剂——特别是甲烷、臭氧、一氧化二氮和氯氟烃 (CFC)。此外，其中一些气体的大气浓度一直以比 CO₂ 更快的速度增长。除了减少使用氯氟烃和化石燃料之外，还没有出现任何策略来应对可能的全球变暖。与其他几个主要环境问题一样，气候变化的某些方面还没有得到很好的理解，在未来很长一段时间内，研究、辩论和行动可能同时发生。

煤炭和其他能源

在中国，煤炭的使用远远超过石油和天然气的使用。国内煤炭基本都进行的是深部开采，所涉及的费用和潜在的危险是相当高的。科学利用煤炭资源的一种方法是将煤炭转化为气态或液态燃料。

煤的气化：在廉价的天然气出现之前，由煤生产的燃气（称为发生炉气）被广泛使用。这种气体是将水蒸气和空气通过红热煤制成的，涉及以下反应：

C(石墨) + H₂O(g) → CO(g) + H₂(g) $\Delta_\text{r}H^\ominus$ = +131.3 kJ mol⁻¹ CO(g) + H₂O(g) → CO₂(g) + H₂(g) $\Delta_\text{r}H^\ominus$ = −41.2 kJ mol⁻¹ 2 C(石墨) + O₂(g) → CO₂(g) $\Delta_\text{r}H^\ominus$ = −221.0 kJ mol⁻¹ C(石墨) + 2 H₂(g) → CH₄(g) $\Delta_\text{r}H^\ominus$ = −74.8 kJ mol⁻¹

主要的气化反应（第一个反应）是高度吸热的。该反应的热量需求通过精心控制的煤的部分燃烧来满足（第三个反应）。典型的发生炉气按体积计含约 23% CO、18% H₂、8% CO₂ 和 1% CH₄ 组成。它还包含大约 50% 的 N₂，因为它的生产过程中使用了空气（氧气来源）。由于 N₂ 和 CO₂ 是不可燃的，所以发生炉气的热值只有天然气的 10% 到 15%。现代气化工艺包括几个改进：

使用 O₂ 代替空气，从而消除产品中的 N₂。
去除不可燃的 CO₂ 杂质和硫杂质，使用 CaO 吸收 CO₂，H₂S 除去 SO₂。
在催化剂的存在下将 CO 和 H₂ 转化为 CH₄（称为甲烷化）。

该产品称为代用天然气 (SNG)，是一种成分和热值与天然气相似的气体混合物。

煤的液化：从煤获得液体燃料的第一步通常涉及煤的气化。随后通过催化反应合成液态烃。

$n$ CO + $(2n+1)$ H₂ → C_nH_2n+2 + $n$ H₂O

或者合成液体甲醇：

CO(g) + 2 H₂(g) → CH₃OH(l)

1942 年，德国约有 1 亿升航空燃料由煤制成。在南非，用于煤液化的 Sasol 工艺一直是汽油和各种其他石油产品和化学品的主要来源。

甲醇

甲醇可以通过一氧化碳和氢气的反应从煤中获得。甲醇也可以通过木材的热分解（热解）产生。按质量计算，甲醇的燃烧热仅为典型汽油的二分之一左右，但与异辛烷（辛烷值 100）和优质汽油（辛烷值 92）相比，甲醇具有较高的辛烷值 (106)。甲醇已经过测试并用可作内燃机的燃料，比汽油燃烧更清洁。甲醇还可用于空间加热、发电、燃料电池，以及作为反应物来制造各种其他有机化合物。

乙醇

乙醇主要由乙烯生产，而乙烯又来自石油。目前的兴趣集中在通过有机物发酵生产乙醇，这一过程在整个有记录的历史中都是众所周知的。通过发酵生产乙醇可能在巴西最为先进，其中使用的植物物质（生物质）是甘蔗和木薯。乙醇在我国用作汽油的添加剂，以提高其辛烷值并减少空气污染。

生物燃料

生物燃料是类似于化石燃料的可再生能源。生物燃料是从死生物材料中提取的燃料，最常见的来源是植物。化石燃料来自已死亡很长时间的生物材料。生物燃料的使用并不新奇，内燃机可使用花生油、乙醇等燃料。生物乙醇来源于大多数糖或淀粉作物（如甘蔗或玉米）中的碳水化合物的发酵。植物油与甲醇可反应产生一类化合物，通常称为生物柴油（脂肪酸甲酯）。柴油是碳数约十六的烷烃，而生物柴油化合物是含有氧原子的碳数差不多的酯（如 19个碳）。柴油和生物柴油的标准燃烧焓非常相近。

尽管生物燃料是化石燃料的有吸引力的替代品，但要广泛使用有几个潜在的缺点。一个主要问题是食物与燃料的问题。用于食品的典型植物（例如甘蔗）是生物燃料的来源，这会推高食品成本。生物燃料的一个积极方面是它们是碳中和的。也就是说，燃烧生物燃料产生的碳然后被植物用于新的生长，导致大气中的碳没有净增加。生物燃料及其使用具有许多其他优点和缺点。重要的是，需要了解这些化合物的化学知识来解决这些问题。

氢

另一种具有巨大潜力的燃料是氢。它最吸引人的特点是：

每克的燃烧热是甲烷的两倍多，是汽油的三倍左右。
与汽油产生 CO 和 CO₂ 不同，其燃烧产物是 H₂O。

目前，商业上使用的大部分氢气是由石油和天然气制成的，但要使氢气成为未来的重要燃料，必须完善从其他来源（尤其是水）中获取氢气的有效方法。以后会讨论生产氢气的替代方法以及以氢气为基础的经济发展前景。

代替能源

燃烧反应只是从材料中提取有用能量的一种方式。我们还看到了另外两种替代能源，生物乙醇和生物柴油。另一种选择是在燃料电池发生电化学反应，使能量以电能而非热量的形式释放（第 19 章）。太阳能可直接使用，无需借助光合作用。核反应可用于代替化学反应（第 25 章）。处于不同开发和使用阶段的其他替代能源包括水力发电、地热能、潮汐能和风能。

7.10 自发和非自发过程：简介

通过应用本章介绍的概念，我们可以量化各种物理和化学过程中涉及的能量变化。在考虑过程或反应的可行性、设计新的合成或比较能源时，化学家通常会借助反应焓来思考。如本章所述，恒压过程中的焓变是需要提供（或预计放出）的热量。

很多反应都朝一个方向自发进行。例如闪亮的铁 (Fe) 管最终会生锈 (Fe₂O₃)。铁生锈的方程式是：

4 Fe(s) + 3 O₂(g) → 2 Fe₂O₃(s) $\Delta_\text{r}H^\ominus$ = −1648.4 kJ mol⁻¹

铁管开始生锈，且会不断锈下去。逆反应（铁锈分解为金属铁和氧气）在自然条件下不会自发发生。在考虑如何解释这些现象之前，我们首先定义术语自发和非自发。

自发过程 (spontaneous process)是发生在一个系统中的过程。反应发生后不需要来自系统外部的任何操作就能继续进行。相反，除非持续进行某些外部操作，否则不会发生非自发过程 (nonspontaneous process)。

一些日常经验可能会使我们相信，系统会自发向低能量状态进行。例如紧紧缠绕的弹簧自然松开以释放其储存的能量；球滚下坡，水向低处流。这些过程的共同特点是系统的势能下降。与过程相关的能量变化（或恒压过程的焓变）是否是确定该过程自发的重要考虑因素？

1870 年代，马塞兰·贝特洛 (Pieltte Marcellin Berthelot, 1827-1907) 和尤利乌斯·汤姆森 (Julius Thomsen, 1826-1909) 独立提出自发变化的方向是系统焓减少的方向在焓降低的系统中，系统会向周围环境散热。贝特洛和汤姆森认为放热反应是自发的。让我们用实际的反应来检验这个假设。

铁的自发生锈是放热的，支持这一假设：

4 Fe(s) + 3 O₂(g) → 2 Fe₂O₃(s) $\Delta_\text{r}H^\ominus$ = −1648.4 kJ mol⁻¹

虽然铁生锈的速度很慢，但它会不断地生锈。结果导致铁的物质的量减少而氧化铁的物质的量增加，直到达到最终平衡状态，此时基本上所有的铁都已转化为氧化铁。逆反应，从氧化铁获得铁单质并非不可能发生，但肯定是非自发的。因此冶炼铁矿石是通过氧化铁和碳反应，而不是直接分解氧化铁。

而如下的反应是吸热的，但也是自发的。这与贝特洛和汤姆森提出的假设矛盾：

Ba(OH)₂·8H₂O(s) + 2 NH₄Cl(s) → BaCl₂(s) + 10 H₂O(l) + 2 NH₃(g) $\Delta_\text{r}H^\ominus$ = 165 kJ mol⁻¹

最简单的例子是 0°C 以上冰的融化和 0°C 以下水的冻结。冰的融化是吸热的，但在 0°C 以上会自发融化。逆过程是放热的，在 0°C 以下自发。

H₂O(s) → H₂O(l) $\Delta_\text{fus}H$ = 6.01 kJ mol⁻¹ H₂O(l) → H₂O(s) $\Delta_\text{fus}H$ = −6.01 kJ mol⁻¹

显然，过程的焓变不是预测自发变化方向的可靠标准。尽管如此，我们还是可以总结出一些结论：

如果一个过程是自发的，则逆过程是非自发的。例如，铁管在空气中生锈是自发的，而铁锈转化为铁和氧气则不是。在高于 0 °C 的温度下，冰的融化是自发的，而水的冻结则不是。
自发和非自发过程都是可进行的，但只有自发过程才会在没有干预的情况下发生。非自发过程要求外部持续进行操作才能进行。
一些自发过程发生得非常缓慢，而另一些则发生得相当快。自发并不意味着反应速度快，铁的生锈剧烈放热但反应非常缓慢。
一些自发过程是放热的，而另一些是吸热的。生成铁锈放热的自发过程。Ba(OH)₂·8H₂O 和 NH₄Cl 的反应是吸热的自发过程。

正如我们将在第 13 章所学习的，过程的焓变是是否自发的一个因素，另一个因素被称为熵。简单地说，熵代表能量的分散性，更具体地说，表示给定数量的能量可以在系统的粒子之间分散的方式的数量。本章讨论的概念（比如说描述和量化各种过程中发生的能量变化）将帮助我们理解和使用熵变来预测自发变化的方向。

近期内容

2 分钟阅读

3 分钟阅读

38 分钟阅读

53 分钟阅读