封面图：一个里德堡分子的电子密度图，看起来就像是一只鲎。里德堡分子包含至少一个处激发态的原子（里德堡原子）。比如说CsCs^*分子，在这里Cs^*的最外层电子被激发到高能级，该分子就是里德堡分子。里德堡分子可以具有非常长的化学键，能达数个微米（一般的化学键仅有数百pm），和巨大的偶极矩（数百德拜）。/©JIN YANG

在上一章我们学习了使用路易斯理论和VSEPR理论对分子形状与结构进行预测，它们只是非常初级的理论，某些情况下需要用更复杂的方法。其中有一种方法涉及原子轨道的杂化，称为杂化轨道理论。另一种方法涉及创建一组属于整个分子的轨道，然后将电子分配给分子轨道。

这些方法都包含有一定的量子力学原理，本章的学习目标不是掌握共价键成键的细节。我们将通过这两个方法进一步了解有关化学键的理论模型。

11.1 成键理论应该做什么

氢分子很适合用来讨论成键理论，想象一下我们将两个相距一定距离的H原子放在一起。相距无限远时原子间不存在相互作用，我们把这个时候的能量定义为0。当两个氢原子相互靠近时，会产生三种类型的相互作用：(1)电子与原子核的相互吸引；(2)电子之间的相互排斥；(3)原子核之间的相互排斥。

如果绘制出两个氢原子组成的系统的能量与原子核距离的关系，所得函数如下图所示。如果原子距离很远，基本不存在相互作用。当原子距离适中时，电子与原子核的相互吸引占主导地位，体系能量下降。在某个特定的核间距下(74 pm)，体系能量最低，为−436 kJ mol⁻¹。随着距离进一步降低，体系能量快速增加。实际分子中核间距会在74 pm附近变化，即原子来回振动，但平均距离为74 pm。这一距离对应的能量就是键解离能的负值。

体系能量与两个氢原子之间距离的关系。从右至左：(1)若间距无限远，没有相互作用，能量定义为0。(2)距离适中时，氢原子相互吸引，能量降低。(3)距离74 pm时体系能量最低，为−436 kJ mol⁻¹。(4)随着距离进一步减少，体系能量迅速增加。 体系能量与两个氢原子之间距离的关系。从右至左：(1)若间距无限远，没有相互作用，能量定义为0。(2)距离适中时，氢原子相互吸引，能量降低。(3)距离74 pm时体系能量最低，为−436 kJ mol⁻¹。(4)随着距离进一步减少，体系能量迅速增加。

成键理论可以解释化学键的参数——键能、键长、键角等。路易斯理论可以定性地判断键级，VSEPR理论可以预测分子键角。这两个理论无法解释或预测键能、键长的定量信息，所以我们需要更为有效的理论。在学习成键理论之前，先考虑一下为什么成键理论都以量子力学为基础。

共价键：量子力学概念

用经典的电磁学理论来考虑共价键是非常方便的——两个原子核相互排斥，而带负电荷的电子就像是『胶水』，将两个原子核粘在一起。然而这种描述是不正确的，如果不使用量子力学原理，就无法解释原子的稳定性（第8章），更别说分子的稳定性了。共价键是一个量子力学的概念，任何不使用量子力学描述共价键的方法都或多或少有瑕疵。但对于本书的读者而言，完全通过量子力学来描述共价键过于困难，所以我们还是继续站在经典物理的角度思考共价键的形成，只不过在其中稍微加入一些在第8章已经学习过的概念。

考虑两个氢原子的系统，如果只考虑势能，两个原子相互靠近应当是势能增加的——外层扩散的电子会相互排斥，导致势能增加。因此仅考虑经典静电力学，无法解释共价键的形成。

现在我们加入第8章学过的电子密度的概念，下面这个示意图中的蓝线是游离氢原子附近电子密度。橙实线是氢分子周围的电子密度，虚线表示橙线相比于两条蓝线之和的差异。

两个H原子放在$z$轴上，蓝线表示H原子垂直$z$轴切面上的电子密度，橙线表示H₂分子垂直$z$轴切面上的电子密度。虚线是橙线相比于两条蓝线之和的差异。

可以看出，形成共价键伴随着核附近电子密度的下降，以及原子核之间电子密度的增加。电子处在两个原子核之间时，静电力趋向于将两个原子核拉在一起，而电子在两个原子核同侧时，其对更近的原子核吸引力更强，趋向于将两个原子核分开。

上图只是示意图，夸大了电子转移到原子核间的量。对于H₂，原子核间的电子密度大概只能增加16%。那这种程度的增加能否获得足够的静电引力形成共价键呢？答案是否定的。体系能量降低的真正原因是电子距离原子核的平均距离减少了，轨道的收缩导致能量降低。

除了电子的势能，还有一个需要考虑的因素是动能。电子的动能会在成键后小幅增加，主要有两个因素改变电子动能。第一个是电子运动的范围，根据德布罗意关系，$\lambda=\frac{h}{p}$，我们可以将动能写为：$E=\frac{h^2}{2m\lambda^2}$。电子运动的空间增大（从一个原子附近到两个原子附近到体积）意味着德布罗意波长$\lambda$的增加，所以动能略微下降。另一个因素是电子距离原子核的距离降低，这会增加电子的动能。综合两个因素，电子动能在成键后增加。

总之，成键涉及电子动能较小的增加，和电子势能相对较大的降低，因此总能量下降。这是量子力学应用在化学键上得出的结论，可帮助我们加深对化学键的理解。

11.2 价键理论

回忆一下在8章学习的氢原子波函数，例如$1s$轨道。两个氢原子相互靠近，轨道发生重叠。当两个原子轨道足够重叠时，便形成了化学键。如果成键是由于电子密度重新分布所导致的，那么其前提就是两个原子轨道相互重叠，电子密度在原子间增加。

通过原子轨道重叠描述化学键的理论称为价键理论(valence bond theory)，重叠的两个原子轨道通常各有一个电子，在成键过程中形成电子对。但也有可能是一个轨道有两个电子，另一个轨道没有电子。

以H₂S为例，根据第8章所学内容，S原子的价电子构型为$3s^2 3p^4$。有一个$p$轨道填有2个电子，另外两个轨道只填有1个电子。这两个轨道分别和一个氢原子的$1s$轨道重叠，形成共价键。价键理论表明H—S—H的键角为90°，这与实验结果92°吻合。

用价键理论描述的H₂S分子，S原子的两个填有单电子的$p$轨道和H原子的$1s$电子形成共价键。

例题

用价键理论描述PH₃分子。

解答

P原子的价电子构型为$3s^2 3p^3$。三个$p$轨道均只填有1个电子，与三个氢原子的$1s$轨道成键。PH₃分子为三角锥形，键角大约为90°。

练习

价键理论描述的PH₃分子与VSEPR理论描述的有什么区别？哪一个更加合理？已知PH₃键角为93°。

11.3 原子轨道的杂化

当我们用价键理论解释甲烷的成键时，出现了一个问题。C的价电子构型为$2s^2 2p^2$，有两个$p$轨道填有一个电子，另一个$p$轨道是空的。所以C应该可以和H形成化学式为CH₂的分子，且键角为90°。但实际上CH₂是一种活性很高的物种，只在特殊条件下才能观察到。

CH₄是一种稳定，正四面体形状的分子，其路易斯结构符合八隅律。要通过价键理论解释甲烷的成键，我们需要四个未成对电子，每个电子都和一个H原子形成共价键。为达到这个目的，我们将$2s$的一个电子激发到空的$p$轨道上：

如果按照激发态的构型形成C—H键，那么有三根C—H键相互垂直（参考PH₃分子），第四根C—H键可指向任何的位置，因为$s$轨道是球对称的。这与实际情况的正四面体不符。为了解释实际分子的形状，我们需要将『老』的四个轨道变成『新』的四个轨道，四个新的轨道指向四面体的四个顶点。

由于原子轨道是一个函数，那么通过函数的线性组合可以得到新的四个函数。这种将原本的原子轨道重新组合产生新的轨道的过程称为杂化(hybridization)。甲烷中一个$2s$轨道和三个$2p$轨道重新组合产生四个$sp^3$杂化轨道(hybrid orbital)。$sp^3$杂化轨道的波函数为：

$$ \begin{align} \psi_1=\frac{1}{2}\left(\psi_s+\psi_{p_x}+\psi_{p_y}+\psi_{p_z}\right)\\ \psi_2=\frac{1}{2}\left(\psi_s+\psi_{p_x}-\psi_{p_y}-\psi_{p_z}\right)\\ \psi_3=\frac{1}{2}\left(\psi_s-\psi_{p_x}-\psi_{p_y}+\psi_{p_z}\right)\\ \psi_4=\frac{1}{2}\left(\psi_s-\psi_{p_x}+\psi_{p_y}-\psi_{p_z}\right) \end{align} $$

下图展示了原子轨道波函数是如何组合成为杂化轨道的：

一个$2s$轨道和三个$2p$轨道线性组合产生四个$sp^3$杂化轨道，$\psi_1$是四个波函数相加获得的，在(1,1,1)方向上具有较大的正值，而在(−1,−1,−1)方向上具有相对较少的负值。 一个$2s$轨道和三个$2p$轨道线性组合产生四个$sp^3$杂化轨道，$\psi_1$是四个波函数相加获得的，在(1,1,1)方向上具有较大的正值，而在(−1,−1,−1)方向上具有相对较少的负值。

氢原子与四个$sp^3$杂化轨道成键，四个杂化轨道的方向就是四面体的形状（想象一下，交错地选取立方体的四个顶点，所得的形状就是四面体），因此杂化轨道+价键理论可以解释甲烷的分子结构。每个杂化轨道都具有25%的$s$成分和75%的$p$成分，杂化轨道的能量应该介于$s$轨道和$p$轨道之间。如果$2s$轨道的能量为$E_{2s}$，$2p$轨道的能量$E_{2p}=E_{2s}+\Delta E$。$sp^3$杂化轨道的能量为$E_{2s}+\frac{3}{4}\Delta E=E_{2p}-\frac{1}{4}\Delta E$。

一个$2s$轨道和三个$2p$轨道线性组合产生四个$sp^3$杂化轨道，杂化轨道的能量介于$2s$轨道和$2p$轨道之间。 一个$2s$轨道和三个$2p$轨道线性组合产生四个$sp^3$杂化轨道，杂化轨道的能量介于$2s$轨道和$2p$轨道之间。

除了$sp^3$杂化之外也有其他的杂化方式，杂化理论广泛用于解释有机化合物和其他分子的成键。在学习其他的杂化方式之前，要强调几点内容：

1. 形成杂化轨道的数量与参与杂化的原子轨道数量相同。除了$sp^3$杂化外，还存在$sp$、$sp^2$杂化。看名字就知道它们分别是一个$s$轨道同一个或两个$p$轨道杂化形成的。
2. 杂化理论是对分子形状的事后解释，没有任何量子力学依据或实验现象表明真正存在杂化轨道。例如我们无法通过电子密度观察到杂化的发生。
3. 对于某些分子，用杂化轨道理论描述成键是不合适的，但对于很多有机物杂化轨道理论非常有用，所以在《有机化学》的学习中还会见到杂化轨道理论。

水和氨中的成键

杂化轨道可以解释H₂O或NH₃的成键。在VSEPR理论中，这两个分子的电子组结构为四面体，而杂化轨道理论认为它们的中心原子进行了$sp^3$杂化。两个理论都得出键角接近于109.5°的结论。实验结果也比较符合，水的键角是104.5°，氨是107°。氨的杂化方式如下：

形成的杂化轨道中，一个填有两个电子，另外三个都有单电子。三个单电子和氢原子形成共价键，而填有两个电子的杂化轨道是N原子上的孤对电子。看起来杂化轨道用于解释H₂O或NH₃的成键非常有效，但光谱实验数据表明$p$轨道并未杂化。这并不难理解：杂化前五个电子的总能量为$5E_{2s}+3\Delta E$，杂化后能量为$5E_{2s}+\frac{15}{4}\Delta E$。杂化的过程能量增加了$\frac{3}{4}\Delta E$。如果不杂化，这两个分子键角应当为90°，与实验不符。一种可能的解释是：因为O—H和N—H具有较大的离子性，带正电荷氢原子的排斥使得键角打开，大于90°。

$sp^2$杂化轨道

元素碳的邻居——硼的价电子层有四个轨道，但只有三个电子。大多数硼化合物中硼以$sp^2$的方式杂化，并留下一个未杂化的$p$轨道。下图展示了这种杂化方式：

$sp^2$杂化符合硼化合物平面三角的形状（例如BF₃分子），$s$轨道和$p_x$、$p_y$进行杂化所得的波函数为：

$$ \begin{align} \psi_1&=\sqrt{\frac{1}{3}}\psi_s+\sqrt{\frac{2}{3}}\psi_{p_x}\\ \psi_2&=\sqrt{\frac{1}{3}}\psi_s-\sqrt{\frac{1}{6}}\psi_{p_x}+\sqrt{\frac{1}{2}}\psi_{p_y}\\ \psi_3&=\sqrt{\frac{1}{3}}\psi_s-\sqrt{\frac{1}{6}}\psi_{p_x}-\sqrt{\frac{1}{2}}\psi_{p_y} \end{align} $$

所形成的三个杂化轨道的朝向夹角为120°，它们具有完全相同的形状，除了角度不同：

$2s$轨道和$2p_x$、$2p_y$轨道杂化，形成三个新的$sp^2$杂化轨道。颜色表示波函数的符号，蓝色为正，橙色为负。 $2s$轨道和$2p_x$、$2p_y$轨道杂化，形成三个新的$sp^2$杂化轨道。颜色表示波函数的符号，蓝色为正，橙色为负。

还有一个$p_z$轨道未参与杂化，其方向垂直于三个杂化轨道所在的平面。

$sp$杂化轨道

一些Be化合物以$sp$的方式杂化并成键。例如气态时的BeCl₂分子为直线形的，$sp$杂化过程的轨道变化如下：

不妨指定$p$轨道为$p_x$，所得杂化轨道的波函数为：

$$ \begin{align} \psi_1&=\sqrt{\frac{1}{2}}\psi_s+\sqrt{\frac{1}{2}}\psi_{p_x}\\ \psi_2&=\sqrt{\frac{1}{2}}\psi_s-\sqrt{\frac{1}{2}}\psi_{p_x} \end{align} $$

两个波函数朝向相反，夹角呈180°。

$sp^3d$和$sp^3d^2$杂化轨道

为描述中心原子电子组数量为5或6的分子，我们需要拓展价层，使用外层的$d$轨道。例如五配位磷化合物PCl₅采用$sp^3d$杂化，杂化轨道的形状为三角双锥。而六配位的硫化合物SF₆采用$sp^3d^2$杂化，杂化轨道的形状为八面体。

如前所述，形成杂化轨道通常意味着能量的增加。$d$轨道的能量远高于同电子层的$s$轨道和$p$轨道，杂化轨道的能量应该相对很高。这进一步表明杂化轨道只是对分子结构的事后解释。

杂化轨道和VSEPR理论

在上一节我们用VSEPR理论预测分子的几何形状，实际上杂化理论比VSEPR理论更早提出。1931年，莱纳斯·鲍林通过杂化轨道的概念解释CH₄、NH₃、H₂O的形状。1940年内维尔·西奇维克(Nevil Sidgwick, 1873-1952)和赫伯特·鲍威尔(Herbert Powell, 1906-1991)首次提出分子的几何构型是由价层中电子对的排列决定的，随后这一想法在1957年被罗纳德·吉莱斯皮(Ronald Gillespie, 1924-2021)和罗纳德·尼霍尔姆(Ronald Nyholm, 1917-1971)发展为VSEPR理论。

VSEPR理论可用于预测分子形状，而杂化理论是对分子形状的事后解释。所以要预测分子的杂化方式，我们首先要使用VSEPR理论预测电子组形状，再根据形状写出杂化方式。

杂化方式	电子组形状	例子
$sp$	直线形	BeCl2
$sp^2$	平面三角	BF3
$sp^3$	四面体	CH4
$sp^3d$	三角双锥	PCl5
$sp^3d^2$	八面体	SF6

例题

XeF₄分子的Xe原子是怎么杂化的？

解答

XeF₄中心原子有6个电子组，分子形状为平面四方。6个电子组意味着$sp^3d^2$杂化。

练习

预测中心原子的杂化方式：Cl₂F⁺、BrF₄⁺。

11.4 多重共价键

价键理论可以用于描述多重键，本节将以乙烯中的碳碳双键和乙炔中的碳碳三键为例。

C₂H₄的成键

乙烯分子有一个碳碳双键，它是平面分子，两个碳原子和四个氢原子都在同一平面上。H—C—H和H—C—C键角均接近于120°。VSEPR理论中碳周围有三个电子组，与实际的键角相符。但VSEPR理论不能解释分子是平面的，而价键理论可以。

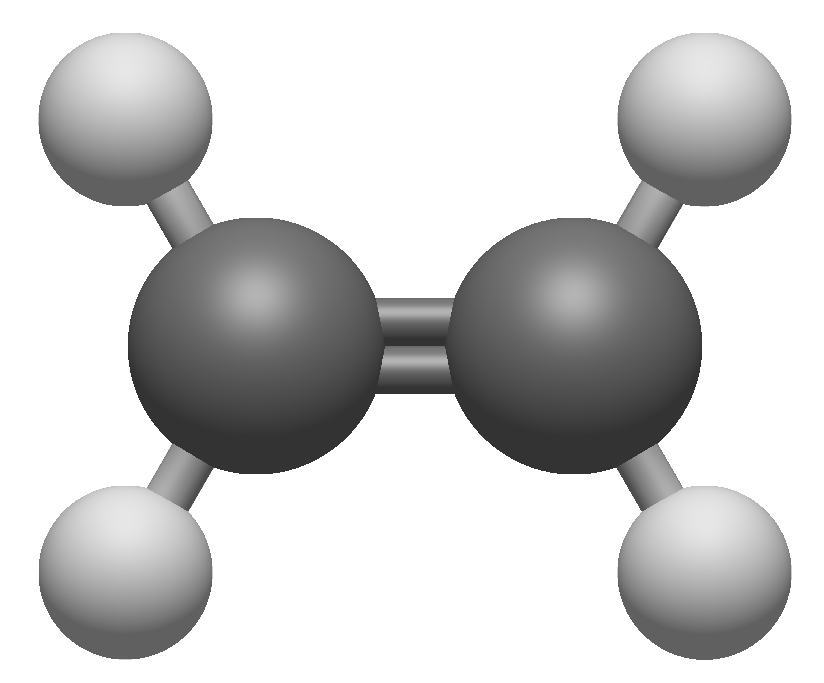
我们来看碳原子是如何杂化的，三个电子组意味着$sp^2$杂化。这一过程如下图所示：

三个$sp^2$杂化轨道中的两个和H的$1s$轨道成键，剩下的一个$sp^2$杂化轨道和另一个碳原子的$sp^2$杂化轨道成键。这样一来，两个碳原子都有一个填有单电子的$p$轨道还未成键。这两个$p$电子相互配对，轨道重叠，形成碳碳双键中的第二根键。

两个碳原子的$sp^2$杂化轨道『头碰头』形成的键称为σ键(sigma bond)，因为沿着连接两个碳原子的延长线的方向看过去，轨道的形状和$s$轨道类似，是圆的。而两个碳原子的$p$轨道『肩并肩』形成的键称为π键(pi bond)，沿延长线方向看过去，轨道的形状和$p$轨道类似。

左上：每个碳原子的两个杂化轨道和两个氢原子形键，余下的杂化轨道互相成键，形成σ键。中上：两个$sp^2$杂化轨道重叠形成σ键的波函数。右上：沿化学键看过去，σ键的形状和$s$轨道类似。左下：碳原子填有单个电子的$p$轨道重叠形成π键。中下：两个$p$轨道重叠形成π键的波函数。右下：沿化学键看过去，π键的形状和$p$轨道类似，具有一个节面。

另一种定义σ键和π键的办法是根据节面的数量：σ键没有节面，而π键有一个节面。上图展示了乙烯中的成键方式，它表明：

• 分子的形状仅由形成σ键的轨道决定。
• 双键的旋转受到限制，转动C—C键会减少$p$轨道的重叠，削弱π键。双键是刚性的，所以乙烯分子是平面的。

此外在多重键中，σ键的重叠比π键要更好。因此碳碳双键(σ+π)的键能(661 kJ mol⁻¹)大于碳碳单键(347 kJ mol⁻¹)，但不是两倍。碳碳三键键能(837 kJ mol⁻¹)也不是单键的三倍。

例题

甲醛(H₂CO)分子是如何成键的？用价键理论描述。

解答

甲醛中C是中心原子，采用$sp^2$杂化，形成三个杂化轨道。杂化轨道和两个H原子的$1s$轨道以及氧原子的$2p$轨道重叠，形成三根σ键。C原子未杂化的有单电子的$p$轨道和O原子另一个有单电子的$p$轨道形成π键。

甲醛应当是一个平面分子，三个$sp^2$杂化杂化轨道处同一平面。

练习

通过价键理论预测二氧化碳的结构。

C₂H₂的成键

乙炔的成键和乙烯类似，乙炔是一个直线形分子。杂化轨道理论认为乙炔的C原子以$sp$的方式杂化，这一过程如下：

C原子的两个$sp$轨道，其中一个和H原子成键，另一个用于形成碳碳σ键。而有单电子的两个相互垂直的$p$轨道则形成两个π键：

左：一个杂化轨道和氢原子成键，另一个杂化轨道用于形成碳碳σ键。右：有单电子的两个相互垂直的$p$轨道形成两个π键。

在已知实验数据的情况下，可以通过数据推测出分子的成键方式。下面这个例题以甲酸为例：

例题

甲酸(HCOOH)又叫蚁酸，一些昆虫在叮咬动物的时候会分泌蚁酸。甲酸是一个平面分子，其键角数据如下图所示：

根据键角数据推断原子的杂化方式。

解答

键角数据表明C进行了$sp^2$杂化（接近120°），而O进行了$sp^3$杂化（接近109.5°）。

练习

笑气（一氧化二氮）的化学式为N₂O，N—N键长113 pm，N—O键长119 pm，键角180°。根据这些信息写出最符合真实结构的路易斯结构。（一些键长数据见第10章）

11.5 分子轨道理论

路易斯理论、VSEPR理论和价键理论都可以用于描述分子的结构，这三个工具用于大多数普通化学课程中涉及的物质都是差强人意的。有些时候我们需要更深入地描述分子的结构与性质，而这三个理论都无能为力，例如解释分子的电子光谱、氧分子的顺磁性、或者为何H₂⁺是稳定的离子。为解决这些问题，我们需要引入另外的理论来描述化学键。

分子轨道理论(molecular orbital theory)基于简单的原子轨道，原子轨道通过线性组合形成分子轨道。分子轨道理论和杂化轨道理论相似的地方在于都涉及原子轨道的重新组合，杂化轨道重新组合的是同一原子的多个轨道，而分子轨道理论则涉及不同原子的多个轨道。本节我们首先从最简单的氢分子开始，然后拓展到同核双原子分子，然后再到多核分子。

回忆第8章学习的内容：原子有一组轨道可用，电子按照能量高低顺序，从低到高填入原子轨道(AO)。类似的，分子也有一组轨道，电子按照能量高低顺序，从低到高填入分子轨道(MO)。与原子轨道不同，分子轨道是分子中所有原子共享的。

我们以F₂的分子轨道计算结果为例，分子轨道展示在下图中。这些分子轨道是通过量子力学计算与波函数分析获得的，计算过程中需要使用薛定谔方程。图中展示了十个分子轨道分子轨道，这些分子轨道分布在两个F原子周围，归整个分子所有。

F₂的分子轨道，轨道按照能量顺序从低到高排列。有一些轨道具有相同的能量，是简并的。这些分子轨道的符号列在右侧，其中*表示反键轨道。 F₂的分子轨道，轨道按照能量顺序从低到高排列。有一些轨道具有相同的能量，是简并的。这些分子轨道的符号列在右侧，其中*表示反键轨道。

分子轨道可以用一种称为原子轨道线性组合(LCAO)的方法来解释，LCAO基于这样的想法：分子由原子组成，原子的原子轨道可作为描述电子如何与所有原子核相互作用的基础。所以原子轨道也可以作为描述分子轨道的基础。用数学的语言说，就是每个分子轨道都能被表示为原子轨道的线性组合。LCAO包括如下内容：

• 每个分子轨道都能被表示为原子轨道的线性组合：当原子组合为分子时，原本存在的一组原子轨道也相应地组合为一组分子轨道。那原子轨道要以何种比例组合形成MO呢？这是个复杂的问题，但对于双原子分子答案比较简单。
• 分子轨道的总数等于组合的原子轨道总数：F原子中的电子分布在五个原子轨道中：$1s$、$2s$、$2p_x$、$2p_y$、$2p_z$，两个F原子一共有10个原子轨道，形成的分子轨道数量也是10个。
• 分子轨道可分为成键、反键和非键轨道：这种分类考虑了轨道的能量变化。原子间电子密度增加通常意味着能量降低——电子同时被两个原子核所吸引——意味着形成了化学键。仔细观察上图，你会发现反键轨道在两个原子核之间存在节面（$\sigma_{2s}^*$轨道），因此反键轨道的能量高于组成该轨道的原子轨道。而成键轨道在原子核之间增加了电子密度（$\sigma_{2s}$轨道），成键轨道能量低于组成该轨道的原子轨道。F₂分子中没有非键轨道，非键轨道的能量相比原子轨道没有显著变化。
• 分子的电子构型是通过将电子以特定顺序放入分子轨道所获得的：电子通过构造原理填充原子轨道。类似的，电子也以相似的原则填入分子轨道——满足泡利不相容原理和洪德最大多重度规则。每一个分子轨道最多填两个电子，且它们自旋相反。电子自旋平行填入简并轨道直到所有简并轨道半满，然后再填充至全满。

我们以H₂的分子轨道来概括LCAO方法。氢原子的$1s$轨道填有电子，$1s$轨道相加($1s_\text{A}+1s_\text{B}$)产生的分子轨道是成键分子轨道(bonding molecular orbital)。该轨道在原子核之间存在电子密度，轨道具有圆柱一样的对称性（沿过两个原子核的轴任意旋转波函数不变）。这一分子轨道记为$\sigma_{1s}$，其能量低于$1s$原子轨道。而两个轨道相减($1s_\text{A}-1s_\text{B}$)产生的分子轨道是反键分子轨道(antibonding molecular orbital)。反键轨道在原子核间存在节面，节面上波函数为0。反键轨道用星号表示，记为$\sigma_{1s}^*$，其能量高于$1s$原子轨道。

H₂分子轨道的电子概率密度。两个原子轨道相加产生成键轨道（左），相减产生反键轨道（右）。圆点是原子核的位置，曲线是过两个原子的线上的概率密度。反键轨道在原子核间存在节面，节面上概率密度为0。

电子填入成键轨道后，能量相比原子轨道下降。而填入反键轨道，能量相比原子轨道增加。稳定的分子应当有更多电子填入成键轨道。在分子轨道理论中，成键轨道每填入两个电子键级+1，而反键轨道每填入两个电子键级−1。键级(bond order)是成键电子与反键电子数量差的一半。

氢分子的分子轨道能级图，两个$1s$轨道组合形成$\sigma_{1s}$成键轨道和$\sigma_{1s}^*$反键轨道。氢分子的两个电子填入成键轨道，体系能量下降。氢分子的键级为1。 氢分子的分子轨道能级图，两个$1s$轨道组合形成$\sigma_{1s}$成键轨道和$\sigma_{1s}^*$反键轨道。氢分子的两个电子填入成键轨道，体系能量下降。氢分子的键级为1。

第一周期元素的双原子分子

现在让我们考虑第一周期元素的双原子分子的分子轨道，它们是H和He形成的一些分子（或离子）。

H₂⁺ 这一物种有一个电子，它填入$\sigma_{1s}$轨道。键级为0.5，相当于半根化学键，这种化学键无法用路易斯理论描述。

H₂ 该分子有两个电子，它们填入$\sigma_{1s}$轨道。键级为1，在路易斯理论中为共价单键。

He₂⁺ 这一物种有三个电子，其中两个填入$\sigma_{1s}$轨道，一个填入$\sigma_{1s}^*$轨道。键级为1 − 0.5 = 0.5，该离子是稳定的。

He₂ 该分子有四个电子，填入$\sigma_{1s}$轨道和$\sigma_{1s}^*$轨道。键级为0，表明分子不稳定。

例题

氢分子的键能为436 kJ mol⁻¹，估算H₂⁺和He₂⁺的键能。

解答

H₂的键级为1，H₂⁺和He₂⁺的键级为0.5，所以键能大约为H₂的一半，即218 kJ mol⁻¹。

练习

Li₂的键能为106 kJ mol⁻¹，那么Li₂⁺的键能是多少？

你认为Li₂⁻稳定吗？

第二周期元素的双原子分子

第一周期的元素形成的分子只需要考虑一个$s$轨道的组合，而第二周期开始情况变得复杂了。第二周期元素的轨道有四个：$2s$、$2p_x$、$2p_y$、$2p_z$。对于多原子分子，$2s$轨道和$2p$轨道能量不同，$2p$轨道能量更高（见第8章）。我们可以假定$2s$轨道只和$2s$轨道组合形成分子轨道，$2p$轨道只和$2p$轨道组合形成分子轨道。那么两个$2s$轨道将产生两个分子轨道，六个$2p$轨道将产生六个分子轨道。

两个$2s$轨道组合产生的分子轨道和$1s$轨道组合产生的分子轨道没有太大区别，只不过$2s$轨道能量高于$1s$，所以产生的$\sigma_{2s}$和\(\sigma_{2s}^*\)轨道要高于$\sigma_{1s}$和\(\sigma_{1s}^*\)。

$p$轨道组合的方式和$s$轨道不一样，轨道组合要满足一定的对称性条件。例如A原子的$2p_x$轨道不能和B原子的$2p_y$轨道组合形成分子轨道，这种组合方式不会导致波函数的净叠加（或净抵消），因此形成的分子轨道能量不会相比原子轨道大幅降低（或增加）。

$2p_y$轨道和$2p_x$轨道组合不会产生波函数的净叠加，形成的分子轨道能量与原子轨道区别不大。

$p$轨道要重叠，最好的方式是『头碰头』形成分子轨道。不妨将连接两原子核的方向定为$x$方向，那么两个$p_x$轨道组合将产生两个σ轨道：$\sigma_{2p_x}$和\(\sigma_{2p_x}^*\)。而两个$p_y$轨道或$p_z$轨道可以『肩并肩』形成四个π轨道。其中两个成键轨道：$\pi_{2p_y}$、$\pi_{2p_z}$，两个反键轨道：\(\pi_{2p_y}^*\)、\(\pi_{2p_z}^*\)。

$2p$轨道组合产生的分子轨道。其中两个$p_x$轨道组合将产生两个σ轨道（最上方的两个），而两个$p_y$轨道或两个$p_z$轨道将形成四个π轨道。 $2p$轨道组合产生的分子轨道。其中两个$p_x$轨道组合将产生两个σ轨道（最上方的两个），而两个$p_y$轨道或两个$p_z$轨道将形成四个π轨道。

轨道的波瓣如果相位相同地重叠，那么将增加原子核之间的电子密度，形成的分子轨道能量更低。如果相位相反，那么将形成反键轨道，能量更高。我们预计$\sigma_{2p_x}$的能量低于任何一个$\pi_{2p}$，因为『头碰头』重叠得更加好。同样，\(\sigma_{2p_x}^*\)的能量也应该高于任何一个\(\pi_{2p}^*\)。

双原子分子的两个π成键轨道应该具有相同的能量——它们是简并的。两个π反键轨道也具有相同的能量。这样一来，我们就获得了在本节刚开始绘制出来的F₂的分子轨道。分子轨道能级图如下：

第二周期同核双原子分子的一种可能的分子轨道能级示意图，图中分子轨道的能量是不成比例的，仅示意出相对能量大小。O₂和F₂具有这样的能级排布。 第二周期同核双原子分子的一种可能的分子轨道能级示意图，图中分子轨道的能量是不成比例的，仅示意出相对能量大小。O₂和F₂具有这样的能级排布。

回到本小节刚开始的假设上来——只有当$2s$和$2p$轨道的能量差足够大，才可以假设$s$轨道只和$s$轨道形成分子轨道。对于第二周期后面的两个元素——O和F来说，这一假设是成立的。但对于第二周期前面的元素——B、C、N而言，$s$轨道和$p$轨道存在相互作用——一个原子的$2s$轨道和另一个原子的$2p$轨道的对称性是相符的，它们可以产生波瓣的净叠加或者抵消。

$2s$轨道和$2p$轨道的混合对原子轨道轨道所形成的分子轨道有影响。由于$2s$轨道相比$2p$能量更低，因此$\sigma_{2s}$能量进一步下降。而$\sigma_{2p}$轨道的能量上升，甚至高于$\pi_{2p}$轨道。B₂、C₂、N₂的分子轨道能级排布如下：

第二周期同核双原子分子另一种可能的分子轨道能级示意图，图中分子轨道的能量是不成比例的，仅示意出相对能量大小。B₂、C₂和N₂具有这样的能级排布。 第二周期同核双原子分子另一种可能的分子轨道能级示意图，图中分子轨道的能量是不成比例的，仅示意出相对能量大小。B₂、C₂和N₂具有这样的能级排布。

O₂和F₂的$2s$和$2p$轨道能量差很大，$s$轨道和$p$轨道不怎么混合，所以轨道能量顺序并没有改变。现在我们获得了第二周期所有双原子分子的分子轨道能级顺序，我们可以按此前学习的规则开始往里面填入电子。对于O₂、F₂以及Ne₂，结果如下：

O₂、F₂和Ne₂的分子轨道填充情况。它们的键级分别为2、1、0。Ne₂键级为0意味着该物种是不稳定的。O₂在$\pi_{2p}^*$轨道上有两个单电子，所以O₂是顺磁性分子。 O₂、F₂和Ne₂的分子轨道填充情况。它们的键级分别为2、1、0。Ne₂键级为0意味着该物种是不稳定的。O₂在$\pi_{2p}^*$轨道上有两个单电子，所以O₂是顺磁性分子。

分子轨道理论可以解释如下的几个事实：

1. 分子的成键强度：O₂、F₂和Ne₂的键级分别为2、1、0。O₂分子有12个价电子，其中8个填入成键轨道，4个填入反键轨道，所以键级为2。我们预计O₂的键能应该强于F₂，而Ne₂键级为0，它应该不能稳定存在。
2. 分子的磁性：具有单电子（未成对电子）的物种具有顺磁性，而电子互相配对的物质是抗磁性的。O₂分子在$\pi_{2p}^*$轨道上有两个单电子，所以它是顺磁性的。
3. 分子失去或获得电子后的变化：以O₂为例，如果它失去一个电子形成O₂⁺，失去的电子是$\pi_{2p}^*$反键轨道的电子，这会导致键级增加。

第二周期其他同核双原子分子的分子轨道填充情况见下图，注意由于$s$、$p$轨道的混合，能级顺序不一样。

第二周期其他同核双原子分子的分子轨道填充情况。它们的键级分别为1、0、1、2、3。Be₂的键级为0意味着该物种是不稳定的。B₂在$\pi_{2p}$轨道上有两个单电子，所以B₂是顺磁性分子。 第二周期其他同核双原子分子的分子轨道填充情况。它们的键级分别为1、0、1、2、3。Be₂的键级为0意味着该物种是不稳定的。B₂在$\pi_{2p}$轨道上有两个单电子，所以B₂是顺磁性分子。

有什么证据支持第二周期同核双原子分子分子轨道的能级顺序不一样？如果不存在$s$、$p$轨道的混合，那么B₂应该是抗磁性分子，而C₂是顺磁性分子。而实验证明B₂是顺磁性的，C₂是抗磁性的。另外的证据来源于光谱学研究，在第8章我们了解到，电子在原子轨道之间跃迁会吸收或放出电磁波（光）。同样的，分子吸收特定波长的电磁波，可以激发分子轨道中的电子跃迁到更高能量的分子轨道。通过分子的电子光谱我们可以获得分子轨道的能级信息。

例题

O₂⁺的分子轨道电子排布是怎什么样的？其键级为多少？

解答

O₂⁺的分子轨道电子排布为：\({\sigma_{2s}}^2\ {\sigma_{2s}^*}^2\ {\sigma_{2p}}^2\ {\pi_{2p}}^4\ {\pi_{2p}^*}^1\)，其键级为2.5级。

练习

N₂⁺和C₂²⁻的分子轨道电子排布是怎什么样的？其键级为多少？

异核双原子分子

异核双原子分子的分子轨道比同核双原子分子要复杂得多，在本章我们只需简单了解。我们以CO为例，首先要确定的第一个问题是C和O原子的$2s$轨道和$2p$轨道的相对能量。随着原子序数增加，$2s$和$2p$电子的有效核电荷均增加，导致轨道能量下降。此外，$2p$轨道是外层轨道，同亚层的电子有屏蔽效应，因此$2p$轨道能量下降的程度不如$2s$轨道。综上，第二周期元素外层轨道的相对能量大致如下：

一些第二周期元素原子$2s$和$2p$轨道的相对能量。从周期表从左往右，$2s$和$2p$轨道的能量差越来越大。 一些第二周期元素原子$2s$和$2p$轨道的相对能量。从周期表从左往右，$2s$和$2p$轨道的能量差越来越大。

CO分子中$s$轨道和$p$轨道是否存在较强的相互作用？从上图中可以看出，C原子的$2s$和$2p$轨道能量接近，而O的$2p$轨道能量介于它们之间，因此O会同时与C原子的$2s$和$2p$轨道组合。所以CO分子的分子轨道排布将类似B₂、C₂这些分子。

CO的分子轨道图如下所示，分子轨道使用简化符号进行标记，如$3\sigma$、$1\pi$。我们把能量最低的$\sigma$轨道记为$1\sigma$，第二低的记为$2\sigma$，依此类推。对于CO的分子轨道，能量顺序为：$1\sigma < 2\sigma < 3\sigma < 4\sigma < 1\pi < 5\sigma < 2\pi < 6\sigma$。

CO的分子轨道能级图，C和O原子的$1s$电子形成的两个σ轨道省略未表示出来。 CO的分子轨道能级图，C和O原子的$1s$电子形成的两个σ轨道省略未表示出来。

从上图可以看出CO的构型为$3\sigma^2 4\sigma^2 1\pi^4 5\sigma^2$。其中$5\sigma$轨道是最高占据分子轨道(HOMO, highest occupied molecular orbital)，即填充有电子的能量最高的轨道。CO分子的键级是多少？我们首先要将分子轨道分为成键、反键和非键。显然$1\pi$轨道是成键的，而$6\sigma$轨道是反键的，因为它们比形成它们的原子轨道能量更低（高）。$4\sigma$轨道和$5\sigma$可以看成是非键轨道，因为$4\sigma$能量和C的$2s$轨道接近，而$5\sigma$和O的$2\pi$轨道能量接近。

这样一来，有6个电子填在成键轨道上，6个电子填在非键轨道上（在这里我们忽略了$1s$电子），分子的键级为3。我们可以通过CO的分子轨道预测NO的键级，NO相比CO多一个电子，该电子会填充在反键的$2\pi$轨道上。所以NO的构型为$3\sigma^2 4\sigma^2 1\pi^4 5\sigma^4 2\pi^1$。其键级为2.5。

例题

写出CN⁻的基态电子构型，并计算其键级。

解答

CN⁻的构型和CO类似，为$3\sigma^2 4\sigma^2 1\pi^4 5\sigma^2$，键级为3。

练习

写出CN⁺和BN的基态电子构型，并计算其键级。

11.6 离域化学键与分子轨道

在11.4节中，我们了解了定域π键。乙烯C₂H₄中的π键归两个C原子『所有』，该π键局限在这两个原子周围。而苯(C₆H₆)中的π键有些不一样，在本节我们将通过分子轨道理论来描述离域π键的形成。

一般来说，分子轨道理论用于多原子分子是非常复杂的，因为难以确定分子轨道由哪些原子轨道组成，以及原子轨道对分子轨道的贡献。在本节我们不需要掌握分子轨道是如何推导的，而只需直接从分子轨道图形中了解多原子分子的成键方式。

苯的成键

苯在1825年被英国科学家迈克尔·法拉第(Michael Faraday, 1791-1867)年发现，科学家很早就知道其化学式为C₆H₆。但直到1865年，奥古斯特·凯库勒(August Kekulé, 1829-1896)才提出还算正确的结构。他认为C₆H₆分子由6个C原子组成单双键交替的六边形环，每个C原子和两个C原子以及1个H原子成键。

乍一看，苯分子中存在两种碳碳键——单键和双键，那么邻二甲苯将有两种异构体——两个甲基中间为单键或者双键。凯库勒认为苯环在两种结构中快速转化，因此无法分离出单一的某种结构。而现代的化学家则认为苯是这两个结构的共振杂化，苯分子的六根碳碳键是等同的。

左：苯的两种共振结构，其真实结构应该是这两个结构的共振杂化。右：邻二甲苯没有异构体，这两个结构表示的是同一个物质。 左：苯的两种共振结构，其真实结构应该是这两个结构的共振杂化。右：邻二甲苯没有异构体，这两个结构表示的是同一个物质。

通过价键理论和分子轨道理论，我们可以更深入地了解苯的成键方式。价键理论认为碳原子以$sp^2$杂化，此外还有一个未杂化的$p$轨道填有一个单电子。碳用一个$sp^2$杂化轨道和H形成σ键，剩下两个杂化轨道与旁边的两个碳原子形成碳碳σ键。这些σ键构成了苯分子的骨架，$sp^2$杂化轨道的键角为120°，也与正六边形的内角相符。

接下来我们考虑C原子的那个未杂化的$p$轨道，$p$轨道的方向垂直于杂化轨道组成的平面，也就是垂直于苯分子所在的平面。六个$p$轨道重叠，形成离域π键(delocalized π bond)。这种π键并不仅限于两个碳原子之间，而是平均分布在六个碳原子之间。为表示这种离域π键，苯的键线式也可以用带内圆的六边形表示。

左：苯中六个C原子的$p$轨道重叠，形成域π键。右：苯的键线式的另一种写法。 左：苯中六个C原子的$p$轨道重叠，形成域π键。右：苯的键线式的另一种写法。

离域π键最好用分子轨道理论来理解，六个C原子的$p$轨道组合形成六个π分子轨道。产生的分子轨道如下图所示，其中三个轨道是成键轨道，三个为反键轨道。

苯的π分子轨道，左：π分子轨道的相对能量；中：π分子轨道的形状；右：分子轨道由对应的$p$轨道组合而成。垂直于分子平面的六个$p$轨道组合形成6个π分子轨道，除了能量最低的轨道，其他轨道在碳原子间均有节面（在分子轨道形状图中用虚线表示）。且节面数量越多，轨道能量越高。 苯的π分子轨道，左：π分子轨道的相对能量；中：π分子轨道的形状；右：分子轨道由对应的$p$轨道组合而成。垂直于分子平面的六个$p$轨道组合形成6个π分子轨道，除了能量最低的轨道，其他轨道在碳原子间均有节面（在分子轨道形状图中用虚线表示）。且节面数量越多，轨道能量越高。

从上图我们可以看出分子轨道是如何通过$p$轨道组合而成的，能量最低的轨道由六个相位相同的$p$轨道组合，相邻碳原子之间没有节面。能量次低的两个分子轨道有一个节面，其中某个轨道的节面穿过碳原子之间，而另一个轨道的节面经过两个碳原子。这两个轨道是简并的（能量相同）。反键轨道具有更多的节面，能量最低的反键轨道有两个节面，而能量最高的轨道有三个节面。

六个$p$电子全部填充在π成键轨道上，π键键级为3。键级是均匀分布在六个C原子之间的，因此可以认为每个C原子之间π键键级为0.5，再加上一根σ键，苯中C—C键的总键级为1.5。其正好是两个凯库勒结构的平均结果。

这六个π轨道均分布在六个C原子附近，这样的分子轨道称为离域分子轨道(delocalized molecular orbital)。可以预计，苯分子平面上方和下方具有较高的电子密度，苯的一些化学性质就与π体系有关。

具有离域化学键的其他结构

现在我们来了解一些其他的具有离域化学键的物种，通常这些物种的路易斯结构只能通过多个共振式表达。例如臭氧的两个共振式：

这两个共振式告诉我们臭氧中O—O键级大约为1.5——两个共振式的平均结果。那么分子轨道理论如何应用于该结构呢？显然，O₃中π键是三个氧原子的$p$轨道共同组成的，每个O原子都贡献一个垂直于O₃平面的$p$轨道，组合形成三个π分子轨道。这三个轨道的形状及能量如下图所示：

臭氧π分子轨道，左：π分子轨道的相对能量；中：π分子轨道的形状；右：分子轨道由对应的$p$轨道组合而成。垂直于分子平面的三个$p$轨道组合形成3个π分子轨道，它们分别具有0、1、2个原子之间的节面。节面数量越多，轨道能量越高。 臭氧π分子轨道，左：π分子轨道的相对能量；中：π分子轨道的形状；右：分子轨道由对应的$p$轨道组合而成。垂直于分子平面的三个$p$轨道组合形成3个π分子轨道，它们分别具有0、1、2个原子之间的节面。节面数量越多，轨道能量越高。

这三个π分子轨道按能量从低到高分别为成键、非键和反键。三个轨道一共填有4个电子，两个在成键，两个在非键。因此臭氧离域π键键级为1，氧原子间平均键级为0.5，总键级为1.5。

例题

NO₃⁻的π分子轨道有一个成键轨道、一个反键轨道。π轨道一共填有6个电子，那么NO₃⁻中N—O键级是多少？

解答

NO₃⁻由4个原子组成，一共有4个$p$轨道，组成4个π分子轨道。所以π分子轨道有一个成键轨道、一个反键轨道，还有两个能量在两者之间的非键轨道。六个电子将成键和非键轨道填满，离域π键的键级为1。因此N—O的键级为1.33。

练习

通过分子轨道理论推测SO₃分子中S—O的键级。

分子轨道理论有什么用？它可以解释为何胡萝卜是橙色，而番茄是红色的。这两种蔬菜中含有的有色物质分别为β-胡萝卜素(C₄₀H₅₆)和番茄红素(C₄₀H₅₈)。

β-胡萝卜素(β-carotene)和番茄红素(lycopene)的结构。 β-胡萝卜素(β-carotene)和番茄红素(lycopene)的结构。

这两个分子最大的特征是连续的π体系（双键），多个连续的$p$轨道组合可以形成很多π分子轨道。这些轨道的能量随着原子个数的增加，大致的关系见下图所示。

多个连续的$p$轨道组合形成π分子轨道，随着碳链的增加，HOMO和LUMO之间的能量差越来越小。 多个连续的$p$轨道组合形成π分子轨道，随着碳链的增加，HOMO和LUMO之间的能量差越来越小。

β-胡萝卜素和番茄红素具有长离域体系，分子HOMO和LUMO之间的能量差远小于普通烯烃，大约在可见光的范围。分子吸收可见光，电子从分子轨道的低能级跃迁到高能级，从而产生颜色。

11.7 分子中的电子密度

第10和11章我们了解了许多成键的理论，从简单的路易斯理论到复杂的价键、分子轨道理论。这些理论都有一些不足之处，本节我们将讨论第10章遗留下来的问题——价层拓展在诸如SF₆、PF₅等分子中是否存在？以及是否应该使用价层拓展来最小化阴离子中的形式电荷，如SO₄²⁻。我们本节将试图用电子密度来解决这些问题。

SF₆的成键

SF₆分子能否不使用拓展价层（即$d$轨道）来描述成键？我们来看下面的几个共振结构：

在这些SF₆的共振结构中，存在四根S—F单键以及两个S⁺ F⁻离子键。因为只含有4根共价键，S周围电子数量满足八隅律。SF₆可以用这些结构的共振杂化来描述。平均来看，S原子带+2的正电荷，而每个F带−0.33的负电荷。这样，通过多个共振式解决了『多余的电子去哪了』的问题。

用这些共振结构描述SF₆是否合理？一种验证的方法是通过量子化学计算S和F所带的电荷。计算结果表明S带+1.79的正电荷，而F带−0.29的负电荷。这说明SF₆中S—F键具有较强的极性，符合上述共振结构。

如果不使用多个共振结构，应该如何描述SF₆的成键？在第10章我们学习了杂化轨道理论，让$d$轨道也参与杂化，形成$sp^3d^2$这样的杂化轨道即可容纳超过八隅律所要求的电子数。这个想法看似很合理（而且在上一章多次用到），但实际上，量子力学计算结果表明SF₆的化学键基本没有$d$轨道的贡献。

电子密度描述化学键

从上面的讨论可以得知，很多具有拓展价层的分子（它们也被称为超价分子）成键同时具有共价键和离子键的特征。我们考虑一个更加简单的分子——SF₂。这个分子可以画出满足八隅律的结构，但该分子中的S—F键也应当具有较多的离子键成分。理论计算结果表明F带−0.35的负电荷，和SF₆类似。通过量子力学计算，获得的三个原子所在平面处的电子密度如下图所示：

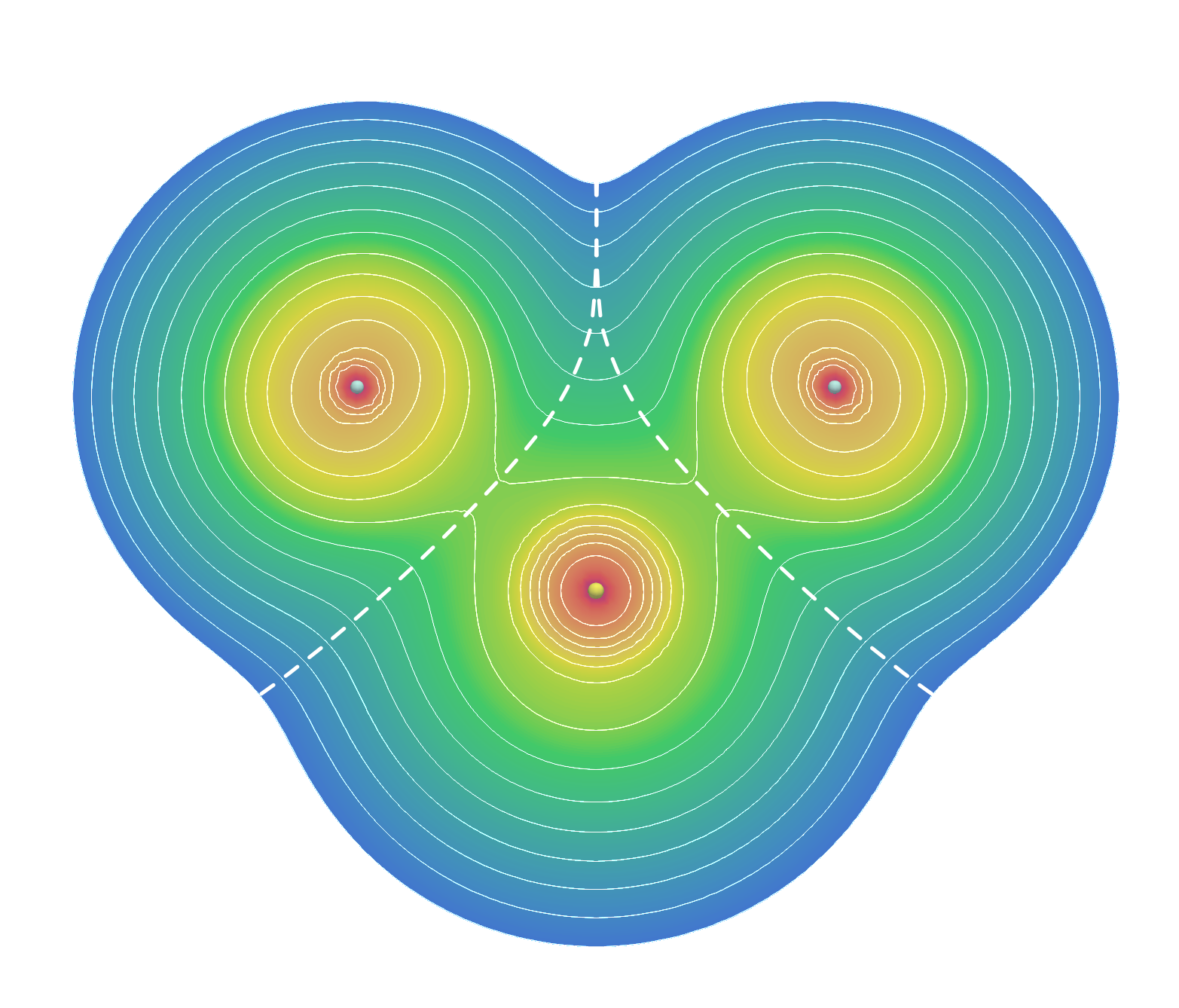SF₂分子的电子密度截面图，截面经过三个原子。细实线是电子密度等高线，最外侧为0.001 au。往里面，等高线取值成倍增加——0.002、0.004、0.008⋯⋯。粗虚线是沿着电子密度尽可能小的路径穿过S—F键的线，可以认为是分子中S原子与F原子的界线。

从图中可以看出，电子密度在原子核附近取最大值。S—F化学键附近电子密度较高，是等高线图的鞍部——往原子核方向电子密度增加，垂直于原子核方向电子密度降低。鞍部的电子密度可以衡量化学键的强弱，密度越大，键级越大。

硫酸和硫酸根的结构

现在我们用电子密度图来考虑是否应当最小化形式电荷——我们将考虑硫酸和硫酸根。它们的等密度面如下所示，这些图包含电子密度等于0.002、0.15和0.20 au的三个等密度面。

SO₄²⁻（上）和H₂SO₄（下）的等密度面，从左至右电子密度依次为0.02、0.15和0.20 au。

从图中可以看出，H₂SO₄分子S=O键电子密度略大于0.20 au，而S—OH键电子密度略小于0.15 au。SO₄²⁻的四根S—O键是等同的，其电子密度介于0.20和0.15 au之间。从电子密度的角度，我们似乎可以得出一个结论：这两个物种的S—O键级顺序应该为：S=O（硫酸） > S—O（硫酸根） > S—OH（硫酸）。

这一结论符合最小化形式电荷的路易斯结构的结果——在H₂SO₄分子中，S=O（末端）是双键，而S—OH是单键。对于存在多个共振结构SO₄²⁻，S—O键级应该是1.5。

然而对分子轨道的分析也表明——$d$轨道并不显著参与硫酸或硫酸根中的成键。硫酸分子中也存在较大的电荷分离——S带+1.32的正电荷，氧原子平均带−0.54的负电荷。也就是说，电荷分离的结构更符合实际的情况。

本章到这已接近尾声，读到这你可能会感觉有些失落，因为本章开头的这些问题看似获得了解释，但也没有完整地回答。不要气馁，这说明我们所学过的结构理论多少有一些局限性。在普通化学课程中，我们主要通过路易斯结构来描述分子，并通过VSEPR理论来确定分子形状。在后续的课程中，你可能会了解一些更复杂但更精确的方法，甚至可以使用计算机来进行分子结构的理论计算。