封面图：哈勃望远镜拍摄的猎户座星云的可见光谱照片，其中红色的光是氢发出的。我们学习的是地球上发现的化学元素，但据推测，这些元素分布在整个宇宙中。/©NASA, public domain

化学是一门研究物质的性质、成分、结构和化学变化及能量变化规律的学科，化学通常研究两种和更多物质相互接触后发生的变化——即化学反应，或一种物质变成另外一种物质的过程。有些时候变化涉及电磁波（光），光负责激发化学反应；也可能是化学反应发出光。

萤火虫体内含有萤光素，在酶的催化下与氧气反应并消耗ATP，可发出绿光，用于求偶/©Jerry Lai CC BY-SA 2.0

有些时候化学并不研究物质之间的反应，例如光谱学研究物质与光的关系，此时并不涉及化学反应。准确的说，化学研究范围包括分子、电子、离子、原子、原子团在内的核-电子体系。很多人称化学为中心科学(the central science)，因为化学涉及人类研究的很多领域，是部分学科的中心。化学是连接物理概念及其他科学之间的桥梁。

中学课程中的化学我们称之为普通化学，普通化学是化学的导论，给初学者提供简单的概念。相比于专业领域，普通化学并不深入和精确，但其提供了直观、图像化的思考方式。即使是专业化学家，仍用这些简单概念解释和思考一些复杂的知识。

最早的化学可认为是人类对火的研究。对当时的人来说，火可以将一种物体变成另一种物体，因此成为了当时人最有兴趣研究的对象。如果没有火，就没有陶瓷、玻璃的制作方式，也无法通过冶炼矿石获得金属。人类在生产、生活的反复试验中，逐渐了解到如何鞣制皮革、酿造酒饮。而现代的化学家则可以生产出许多自然界不存在的材料，合成药物、纤维等天然或人造物质。早期的化学知识包括通过反复实验总结出的操作方法，而现代科学是系统性的知识体系。为了获取新的知识，我们使用一套称为科学方法(scientific method)的技术。

1.1 科学方法

科学探究是指科学家研究自然世界并根据他们的工作得出的证据提出解释的多种方式。古希腊时期亚里士多德提出推理的三种方案：溯因、演绎以及归纳。从某些基本假设开始，通过演绎的方法可获得逻辑结论：例如如果有$a=b$，$b=c$，那么$a=c$。单纯的演绎不足以获得科学知识，无法解决特定的科学问题。亚里士多德假定存在四种基本物质（四元素）：空气、土、水、火，他认为所有其他材料都是这四种基本物质组成的。炼金术士希望可以将铅变成金，所有的尝试最终均徒劳无功——因为四元素的假设是错误的。

现代的科学方法源于17世纪，由伽利略、弗朗西斯·培根、罗伯特·波义耳和艾萨克·牛顿等人创立。科学方法是进行科学的过程，科学建立在先前知识的基础上，并随着时间推移产生更深入的理解。研究科学的流程并不是一成不变的，化学是一门以实验为基础的自然科学，但随着计算化学的发展，越来越多的化学发现是理论预测在先，而实验证明在后。总之，现代科学家的研究流程原比本文接下来介绍的要复杂。一个有代表性的科学方法的步骤如下：

在观察自然现象后，我们会提出问题，问题可以是具体的，如『为什么真金不怕火炼，而其他金属烧过后表面会变灰变黑』，也可以是开放性的，如『如何低成本地将海水变成淡水』。假设(hypothesis)是在提出问题的基础上，或许可以解释该问题的知识。假设可以是具体的，如『金不与空气反应，而其他多数金属可以与空气反应』；也可以是宽泛的，如『某些物质只允许淡水通过，不允许海水通过』。科学假设必须是可证伪的，这意味着我们可以通过实验确定假设是否正确。

古埃及法老图坦卡蒙(BC 1341-1323)的金面具，经过三千多年后依然闪亮。金的性质稳定，不仅不与空气反应，对许多腐蚀品也是化学惰性的/©Tammy Cuff

如果假设是正确的，根据逻辑推理可产生一个或多个预测。越多的预测被实验证实，则表明假设越具有说服力，我们将通过实验检验的预测称为理论(theory)。理论可以进一步解释自然规律或预测自然现象。但多个理论相互冲突时，通常我们保留预测最成功或者假设最少的理论。大多数理论随着时间推移会被进一步修改，或是废弃。

路易斯·巴斯德(Louis Pasteur, 1822–1895)写道：Chance favors the prepared mind（机会只青睐有准备的头脑）。许多科学发现是偶然的，1928年亚历山大·弗莱明(Alexander Fleming)在撰写一篇关于葡萄球菌的会议论文。七月下旬有一些霉菌孢子意外落入葡萄球菌的培养皿中。八月份弗莱明回乡下度假，直到9月3日返回实验室，他才发现青霉菌污染。青霉菌杀死了附近的细菌，这一现象引起了弗莱明关注，最终导致青霉素的发现，改变了人类和传染病之间斗争的历史。

1.2 物质的性质

『化学是一门研究物质的性质、组成⋯⋯的学科』，本章开头就提到了三个术语：物质、性质、组成。

物质(matter)是任何具有质量的物体，且其通过体积占据空间。我们周围所有看到、摸到、闻到的物体都由物质组成。空气也是一种物质，尽管我们看不到这些气体；而灯光不是物质，其是一种形式的能量。

性质(property)是物质的属性，可用于区分不同的物质。物质的性质分为两大类：物理性质及化学性质。

成分(composition)是物质的组成内容及相应比例。水由氢和氧组成，以重量(wt)计含11.19 wt%的氢和88.81 wt%的氧。过氧化氢是一种常用的漂白剂和消毒剂，也由氢和氧组成，但成分不同——过氧化氢含5.93 wt%的氢和94.07 wt%的氧。

物理性质和物理变化

物理性质(physical property)是不改变其组成的情况下物质所表现出来的属性，例如铝可以被捶打成薄片或拉成细丝，这种性质称为延展性；铝是热和电的良导体，用于制作散热器、电线。

在物理变化(physical change)中，物质的物理性质发生变化但成分不变。冰化成水或水结冰会导致物理性质改变，但无论是水还是冰，其成分是一样的：都含11.19%的氢和88.81%的氧。

正在融化成水的冰锥。冰是一种固体，而水是一种液体，两者物理性质相差很大，但成分一致/©M. Maggs

化学性质和化学变化

在化学变化(chemical change)或化学反应(chemical reaction)中，一种或多种物质转化成具有不同成分的新物质。判断是否是化学反应的关键是成分的变化。木炭的燃烧涉及化学变化，木炭的主要成分是碳，而木炭燃烧后得到的是二氧化碳气体。化学性质是物质样品在所给条件下发生（或不发生）反应的能力。

用于烧烤的锡箔纸实际上是铝箔，因为锡具有一定毒性，现已不用于食品包装。铝和锡均具有良好的延展性和导热性。木炭在空气中燃烧，其与空气中的氧气发生化学反应，产生二氧化碳并放出大量能量。而铝箔在这种条件下并不燃烧/©LUM3N

在空气中点燃镁会发出耀眼的白光，人们利用这一反应制造烟花、闪光弹。而铝和铁在空气中仅表面氧化，不会燃烧。镁、铝和铁都是银白色闪亮的金属，是良好的热导体与电导体，它们的部分物理性质相似，但化学性质(chemical property)不同，镁甚至可与与热水反应。因此铁和铝广泛用于制造建材，如金属水管，而镁不可以。

镁粉用于制作烟花，通过粘合剂将镁粉固定在铁丝上，点燃后会发出耀眼的白光。而铁丝在高温下变成暗红色，并不燃烧/©PublicDomainPictures on pixabay

物质的性质决定了它们的用途，铜、银、金被称为货币金属，某些国家的货币曾经建立在金本位上。这不仅是因为金较为稀有，且具有独特的颜色，更是因为金的化学性质稳定，可以长久保存。

1.3 物质的分类

物质由称为原子(atom)的微小单元组成，不同种类的原子组成了不同的元素(element)，目前国际纯粹与应用化学会(IUPAC)一共认可118个元素，它们都有自己的名称与符号。一些元素是我们熟知的，如碳、铁、金，而另一些并不常见，如铥和氪。其中98种元素可以在自然界找到，尽管某些元素的含量极其微量，而剩下的20种元素是人工合成的。这些元素以一定规律排列在表中，称为元素周期表，将在下一章中学习。

目前公认的118个元素按一定方式排列为元素周期表/©Siriudie 目前公认的118个元素按一定方式排列为元素周期表/©Siriudie

化合物(compound)是两种或多种元素以固定比例结合在一起的化学物质，截止2015年，人类已经发现了1434万个化合物。每年新发现的化合物数量$s_t$大致按指数的方式增长：$s_t=51.85e^{0.04324(t-1800)}$，按此趋势到2023年人类将发现超两千万种化合物^来源。某些化合物可以分离出一个个的分子(molecule)，分子是与化合物具有相同元素组成比例的最小实体。水由水分子组成，一个水分子含两个氢原子和一个氧原子；而一个过氧化氢分子含两个氢原子和两个氧原子。肌联蛋白是已知最大的蛋白质，人体中的肌连蛋白约由53.9万个原子组成。

元素单质和化合物样品的任何部分成分都是一致的，我们称其为纯净物(substance)。而含有多种物质的样品称为混合物(mixture)，若混合物的成分和性质是始终一致的，则被称为均相混合物(homogeneous mixture)或溶液(solution)。生理盐水是氯化钠（食盐）溶于水形成的溶液，一瓶生理盐水的任何部分尝起来都一样咸。海水也是种混合物，溶解的盐主要是氯化钠，海水比生理盐水更咸，因为溶解的氯化钠更多。

非均相混合物(heterogeneous mixture)不同区域（相）的组成不一样，物理性质也不同。沙子和水混合后沙粒沉到底部，泥水、酱油、牛奶、树叶都是非均相混合物。

混合物的分离

可以通过适当的物理方法分离混合物。粗盐中含有泥沙等不溶性杂质，将粗盐溶于水得到浑浊的液体。这些液体倒入放有滤纸的漏斗中，泥沙会留在滤纸上，而溶液流入漏斗下方的烧杯中。这种操作称为过滤(filtration)，过滤无法将溶解在水里的盐和水分开。

为了从上述溶液中获得精盐，我们可以将实验溶液煮沸以蒸发除去大部分水。这一过程中逐渐有氯化钠固体析出，蒸发到一定程度后冷却混合液，过滤分离剩余的少量溶液和氯化钠固体，便得到了精盐。如果在蒸发的过程中同时收集挥发的水分，这一过程称为蒸馏(distillation)。

不能相互溶解的液体之间可通过分液的方式分离，而相互溶解的液体可通过分馏(fractional distillation)的方法分离（见第14章）。一种现代的分离方法叫色谱(chromatography)，其利用不同物质在固体表面吸附强度的差异进行分离。下图的薄层色谱(TLC)实验可以看出墨水中含多种不同颜色的色素。

黄色和蓝色墨水混合得到绿色墨水，烧杯中右二是两种墨水的混合，可通过薄层色谱分离开/public domain

化合物的分解

将混合物分离成纯净物通常比将化合物分解为元素要简单得多，从铁矿石（氧化铁）中提取铁需要工业高炉；从海水中获得氯化镁，并从中提炼镁需要消耗大量电力。通过化学反应将化合物分解为其他化合物通常更加简单，焦糖是糖加热部分分解得到的深色物质，如果加热的火候没掌握好，则会发生碳化。

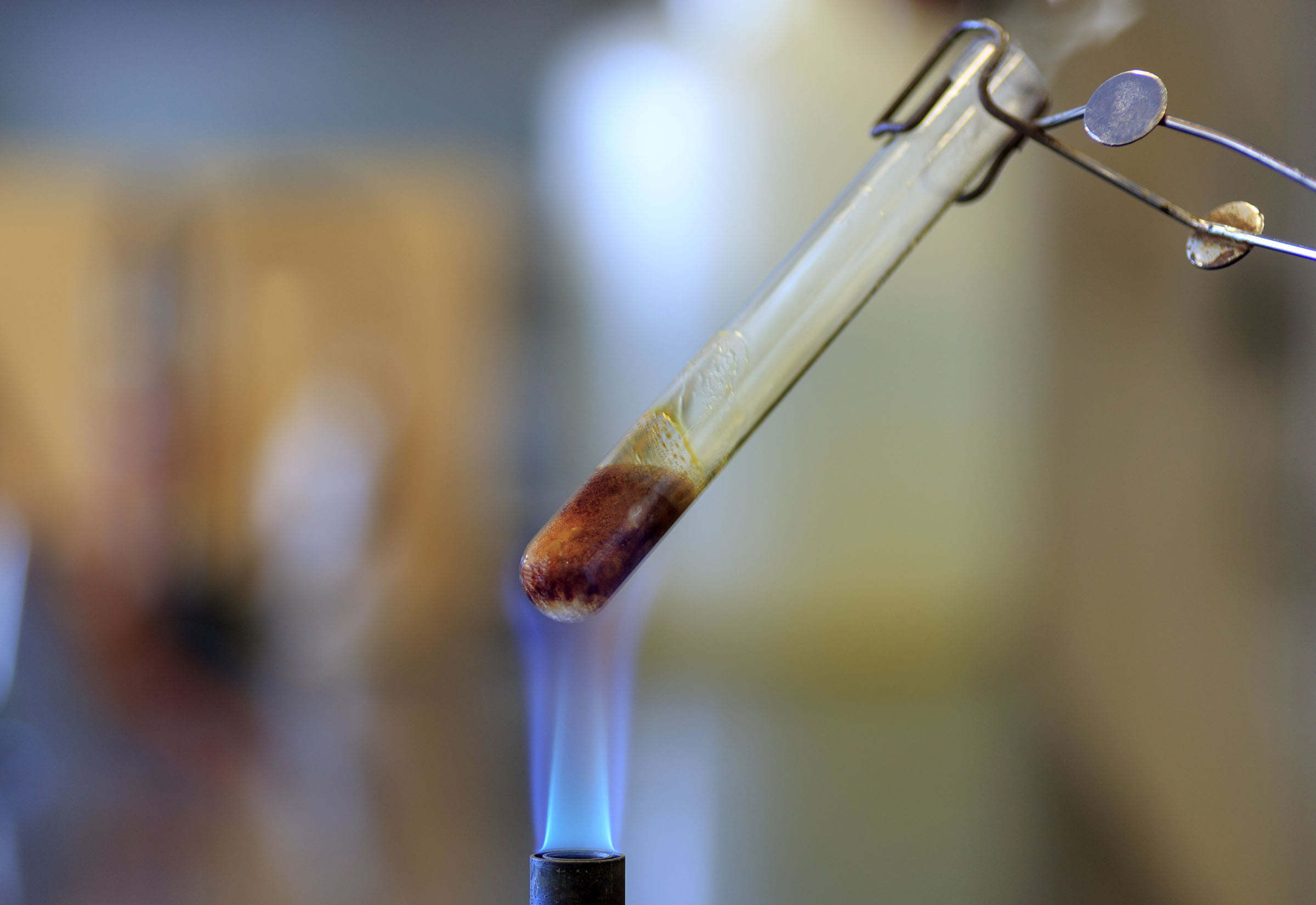加热蔗糖会导致蔗糖分解成焦糖（一种复杂的混合物）和水，进一步加热最终会得到碳元素，希望这种事情不要在厨房发生/public domain

物质状态

物质通常以三种状态存在：固态(solid)、气态(gas)和液态(liquid)。固体中微粒紧密接触，有时会排列成有规则的结构，称为晶体(crystal)。液体中微粒之间的距离相比较远，微粒可以自由移动，这赋予液体流动的性质。气体中的微粒相距远得多，气体总是膨胀并充满整个容器。物质可以以多种状态存在，冰水中水以固体和液体的形式存在，而一壶滚水则同时存在液态水和水蒸气。

南极的一角，图中水以三种状态存在：固体、液体以及我们看不见的水蒸气（更精确的说，是水蒸气和空气的混合物）/©Martin Fuchs

宏观尺度(macroscopic scale)是指是指可以用肉眼直接看到的尺度，一块冰、一壶水是宏观层次的物体。微观尺度(microscopic scale)则涉及原子和分子——这些常规显微镜都无法看见的微粒。

1.4 SI单位制

化学是定量的科学，我们会将物质的性质与已知的标准量进行比较，得到某个数与单位的乘积。我们说一个人身高是160厘米，是指身高相当于厘米这个标准长度的160倍。我们将在本节学习一些对于化学家很重要的基本单位。

国际单位制（法语：système international d'unités）缩写为SI，是现代的公制单位，是国际通用的测量系统。其包括七个基本单位，并从这七个基本单位派生出许多个导出单位。

物理量	单位（简称）	符号
长度	米	m
时间	秒	s
质量	千克	kg
温度	开尔文（开）	K
物质的量	摩尔（摩）	mol
电流	安培（安）	A
光强	坎德拉（坎）	cd

SI是十进制系统，与基本单位相差10的幂的数量用前缀来表示，例如厘米(cm)、毫米(mm)是加了前缀的米(m)。SI前缀表如下：

单位	词头	单位	词头
1018	艾(E)	10−1	分(d)
1015	拍(P)	10−2	厘(c)
1012	太(T)	10−3	毫(m)
109	吉(G)	10−6	微(μ)
106	兆(M)	10−9	纳(n)
103	千(k)	10−12	皮(p)
102	百(h)	10−15	飞(f)
101	十(da)	10−18	阿(a)

今后接触的大多数物理量都是用SI单位表示的，SI单位之间的转换非常常见，例如从千克(kg)到克(g)。有些时候我们会接触非SI单位，此时需要在数值上乘以或除以一个转换因子。

时间

时间(time)的基本单位是秒(s)，但生活中主要使用秒、分、时、天及年做为单位，取决于用于表述短间隔还是长间隔。这些生活中的单位也在科学研究中使用。最初秒基于一天的长度，但其并不是恒定的，因为地球自转速度会发生变化。一秒曾经被定义为1900年长度的1/31,556,925.9747，现在我们使用原子钟这种极其精确的仪器，一秒定义为元素铯的某种原子（铯-133）发出特定辐射的9,192,631,770个周期所需的时间。

超稳定镱晶格原子钟。镱原子在烘箱（左侧的大金属圆柱体）中产生，并被送到图片中间的真空室，由激光操纵和探测。激光通过五根光纤（例如照片下方中间的黄色光纤）传输到时钟/©Burrus-NITS

长度

长度(length)的基本单位是米(m)，最初其定义为赤道到北极距离的1/10,000,000，并将其转化为国际米原器——一个用铂铱合金制成的X形长棍。过去一米的长度被定义为国际米原器的长度，这个方案并不好，因为棒的长度会随温度变化而变化，且不能准确复制新的米原器。现在我们定义一米是光在真空中一秒传播距离的1/299,792,458。

用90%铂和10%铱构成的合金制成的国际米原器，米在当时被定义为在冰水混合物的温度下国际米原器上两道细线之间的距离/public domain

质量

质量(mass)描述了物体中物质的数量，SI单位下质量的单位是千克(kg)，对一般的化学反应而言是个较大的单位，我们更常用的是克(g)。最早千克定义为在冰的熔点时一立方分米水的质量，由于其难以精确测量，后更改成国际千克标准原器的质量。2019年，千克的定义再一次修改，现在规定普朗克常量为6.626,070,15×10⁻³⁴ kg m² s⁻¹，也就是说千克的定义依赖于米和秒。在日常生活中，质量和重量经常互换使用。重量是重力作用在物体上的力，在地球上相同的地点，重量和质量成正比，数学上表示为：$W\propto m$或者$W=g\times m$，$\propto$是正比于符号。由于重力加速度$g$因地而异，物体的重量也因地而异，但质量相同。

最常见的测定质量的设备称为天平。实验室有两种天平，一种是横梁天平，砝码放在臂一端的盘上，另一端放待称量物质。而现在更常用的是电子天平，其原理是通过电磁力抵消待测物体的重力，物品放在天平上，重力会打破平衡，从而需要更强的电流重新平衡。增加的电流强度与重量成正比，并转换成天平上的读数。

温度

为了建立温标，我们设置某两个温度为固定值，并将其等分。在一个大气压下，我们将冰融化的温度设为0 °C，而水沸腾的温度设为100 °C，中间等分为100份，这样就得到了摄氏温标(Celsius scale)，每等分称为一摄氏度。华氏温标(Fahrenheit scale)定义冰的熔点为32 °F，沸点为212 °F，并分为180份。

SI温标是开尔文温标(Kelvin scale)，零值是最低可能的温度，为0 K，其等于−273.15 °C。开尔文温度会在第六章再进行学习，现在只需了解以下几点信息：

• 开尔文温标的单位是开尔文，其大小与摄氏度相同
• 开尔文温标不需要加符号°，常压下冰在273.15 K融化，不能写成273.15 °K
• 开尔文温标又叫绝对温标，平衡态体系不存在负开尔文温度

我们通常使用摄氏度为单位，但在进行某些计算时需换算成开尔文温度。华氏度在部分国家以及相应的工程上有使用，需要掌握换算的方法。

例题

人体正常体温范围是36.1~37.5 °C，这一范围如何用华氏度表示？

解答

将摄氏度转化为华氏度的方法是：$t(^\circ\text{F}) = \frac{9}{5}t(^\circ\text{C})+32$，因此36.1~37.5 °C等同于97.0~99.5 °F。

练习

一本美国的烹饪书上写道，烤箱烤肉的温度应该是350 °F，其等于多少摄氏度？

导出单位

除了七个基本SI单位，还有许多的测量属性表示为这七个基本单位的组合，称为导出单位。例如车辆速度是距离除以所用的时间，即速度的单位是长度除以时间，如m/s或m s⁻¹。某些导出单位具有特定的名称，例如kg m⁻¹ s⁻²称为帕斯卡Pa（见第六章），kg m² s⁻²称为焦耳J（见第七章）。体积也使用导出单位，SI标准下的体积单位是立方米m³，这是个较大的单位，更常见的是升L和毫升mL。1 m³ = 1000 L = 10⁶ mL。

非SI单位

在SI单位普及前，世界各地有各自习惯的单位。我们现在仍然使用斤和两用于计算重量，亩用于测量土地面积。香港的房屋面积使用平方英尺，而不是平方米。少数几个非SI单位在课程中使用：用于衡量气压的毫米汞柱mmHg或托Torr、表示微观体系长度的埃Å、表示分子偶极矩的德拜D等。

1.5 密度和百分含量

上一节我们了解了导出单位，密度是很重要的导出单位。本节将学习两个今后经常用到的量：密度和百分含量。

密度

一斤棉花和一斤铁哪个重？如果你回答两者一样重，说明你清楚重量的含义。任何回答铁比棉花重的都混淆了重量和密度(density)的区别，日常生活中我们会用重来表示物体密度大，但在科学领域显然不能这样做。密度大的物体物质更加集中，也就是同样一斤的铁块，铁中的物质被限制在更小的体积内，铁比棉花更为致密。密度是质量和体积的比值：$d=m/V$。

质量和体积都是广延性质（广度性质, extensive property），广延性质会随着系统大小或物质多少而发生改变。质量除以体积得到密度，密度是强度性质(intensive property)，强度性质与系统大小或物质多少无关。强度性质对化学家很有用，其可用于鉴别物质。

用SI基本单位表示的密度应当为千克每立方米，kg m⁻³，化学家更常用克表示质量，毫升或立方厘米表示体积，此时的密度为克每毫升g mL⁻¹或克每立方厘米g cm⁻³。4 °C时水的密度为1.000 g mL⁻¹，也就是说一升4 °C的水质量为一千克。20 °C时水的密度约为0.9982 g mL⁻¹，这说明密度是温度的函数——温度变化导致体积变化，但质量不变，使得密度发生改变。

固体的密度也与温度有关，相比于气体，液体及固体的密度和温度关系并不显著。固体和液体的密度相比气体大得多，物质通常的密度范围如下：

• 固体：0.2~20 g cm⁻³
• 液体：0.5~4 g cm⁻³
• 气体：通常几克每升

一般来说液体的密度相比固体更精确，因为固体的微观结构可能存在缺陷。固态纯净物的密度相比混合物更加精确。

物理里面我们学过：密度小于液体的固体会浮在液体表面上，并排开与自身质量相等的液体；密度大于液体的固体会沉在底部，并排开与自身体积相同的液体。彼此不混溶的液体将分为不同层，密度最大的液体在底部，密度最小的在顶部。

密度的测量

通过测量物体体积和质量，并将其相除，就得到了密度。反之，若知道物体的密度，则可以根据体积确定物体的质量或根据质量计算体积。例如汞在25 °C下的密度为13.5 g mL⁻¹，1 kg的汞体积为多少？此时涉及三个步骤的转换：

kg 汞 → g 汞 → mL 汞

第一步使用系数1000 g/kg，第二步使用密度将质量转化为体积：1 mL = 13.5 g。因此最终体积为：1.000 kg × 1000 g/kg × 1 mL/13.5 g = 74.1 mL。

例题

不锈钢的密度为7.75 g cm⁻³，要从直径为2.54 cm的钢棒上切下一个质量为1.00 kg的圆柱体，需要截取多长的钢？

解答

假设钢的长度为$x$ cm，那么有$1.00\times10^3=\frac{\pi d^2l}{4}\rho=\frac{3.1416\times2.54^2\times7.75}{4}x$，解得$x=25.5$。即截取25.5 cm的钢棒。

练习

一块煤在悬挂在弹簧秤上，并称重两次。在空气中秤的读数是156 g；煤块放入20 °C的水下，秤的读数为59 g。煤的密度是多少？以g cm⁻³表示。已知水在20 °C下的密度为0.9982 g cm⁻³。

百分含量

成分是物质的组成内容及相应比例，成分可用于识别不同的物质样品，我们可以通过百分含量来表示成分。顾名思义，百分含量是将整体分为100份，某一成分所占的数量，即百分比。海水含3.5%质量分数的氯化钠，说明每100 g海水中含有3.5 g氯化钠。水中氢的质量分数为11.19 %，过氧化氢中氢的质量分数为5.93 %。因此相比于过氧化氢，水中含有更多的氢（当然，更少的氧）。

例题

可以通过蒸干海水提取氯化钠，已知海水中氯化钠的质量分数为3.5%，海水的密度是1.03 g mL⁻¹，要获得45 g氯化钠，至少需要多少毫升的海水？

解答

假设需要$x$ mL海水，有$1.03\times0.035 x=45$，解得$x=1248$，即需要1248 mL海水。

练习1

疫情期间酒精（乙醇）消毒液短缺，张三打算通过蒸馏白酒获得乙醇质量分数为70%的消毒液。白酒中乙醇的质量分数是31%，酒的密度为0.952 g mL⁻¹。从8瓶500 mL的白酒中最多可以获得多少质量的消毒液？

练习2

由于缺少蒸馏装置，张三决定混合乙醇质量分数为96%的伏特加和乙醇质量分数为42%的二锅头得到乙醇质量分数为70%的消毒液。商店只有2瓶500 g的伏特加，为了获得尽可能多的消毒液，他应该购买几瓶200 g装的二锅头？最多可以获得多少质量的消毒液？

1.6 科学测量中的不确定度

所有测量均存在误差(error)，误差是测量结果偏离真实值的程度。测量仪器本身的固有的误差称为系统误差(systematic error)，例如厨房温度计可能比真实温度高1 °C。而随机误差(random error)是其他无法控制的因素导致数据随机分布的误差，例如多次测量一个人的身高，因站立姿势的略微不同使得结果也略有差异。因某些人为因素，例如未阅读仪器说明书导致操作错误，使得测量结果太低或太高，这种情况称随机错误，不是误差。

精密度(precision)是测量数据再现性的程度。多次测量得到的数据相互之间越接近，则精密度越高。相反，若相互之间存在较大偏差，则精密度较低。准确度(accuracy)是测量值与接受值或真实值的接近程度，高精度测量并不一定是准确的，比如方法存在较大的系统误差。尽管如此，科学家通常追求高精度的测量。

电子天平有两种类型，一种是精度较低的台秤，最小单位一般在0.1~0.01 g之间。另一种是高精度的分析天平，最小单位一般是0.0001 g。现有一样品，用台秤和分析天平分别测量三次，数据如下：

	台秤	分析天平
第一次	1.23 g	1.2328 g
第二次	1.24 g	1.2327 g
第三次	1.22 g	1.2329 g
平均值	1.23 g	1.2328 g
再现性	±0.01 g	±0.0001 g
精密度	低	高

台秤获得的数据小数点后有两位，而分析天平获得的数据小数点后有四位。台秤称量结果的分散性大于分析天平，因此分析天平具有更高的精密度。

1.7 有效数字

在台秤测量得到的结果为1.22，1.23及1.24 g，最终取平均值1.23 g。这些结果的前两位数字是确定的，而最后一位数字是不确定的。科学家会将结果记作1.23±0.01 g或者1.23(1) g。我们称这个结果具有三位有效数字，而分析天平称量的结果记做1.2328(1) g，其具有五位有效数字。有效数字(significant figure)的数量表示测量仪器的精密度。

一个数据具有多少位有效数字？我们通过如下规则来判断。

• 除零以外的任何数字都是有效的。例如12.378有五位有效数字
• 最开始的零是无效的，第一个非零数字之后的零都有效。例如0.01708具有四位有效数字
• 整数后面的零是不明确的。例如1500的有效数字可能是两位、三位也可能是四位。

为了避免有效数字不明确，我们可以使用科学计数法来表示。1500可以写成1.5×10³、1.50×10³或1.500×10³，这三种写法分别具有2，3，4位有效数字。

有效数字的运算

计算过程既不能额外获得精密度，也不能随意丢弃精密度。有多种方法用于确定如何正确表示结果的精密度，目前的学习中使用有效数字规则进行计算即可。

乘法或除法运算的结果以有效数字最少的数为标准，最后保留与之相同的有效数字位数。

一个长方体铁块，用游标卡尺测量其长宽高，分别为12.67，10.02，8.30 cm。因此铁块的体积为：

12.67_{四位有效数字} × 10.02_{四位有效数字} × 8.30_{三位有效数字} = 1.05×10³_{三位有效数字}  (cm³)

对于加减法，规则如下：

加法或减法运算中，将所有数对齐后相加或相减，结果保留有效数字至最靠前的数。

考虑计算三个数的和：9876.5，135.71，8.704。对齐小数点后，有效数字最靠前的数是9876.5。因此结果保留至小数点后1位。

9876.5_{五位有效数字} + 135.71_{五位有效数字} + 8.704_{四位有效数字} = 10020.9_{六位有效数字}

注意结果的有效数字比任何项都要多，在加减法中是允许的。此外某些数字不受有效数字规则限制，主要有两种情况：

• 定义量，例如1 min = 60 s，普朗克常量为6.626,070,15×10⁻³⁴ kg m² s⁻¹
• 数量，如水分子含两个氢原子，立方体有六个面

另一个特殊的情况是对数值，其有效数字从小数点后开始计算。例如某一水溶液的pH = 2.74，意味着氢离子的浓度为10^−2.74 mol L⁻¹。这一结果有两位有效数字，即1.8×10⁻³ mol L⁻¹。

进舍规则

计算结果为1054，为保留三位有效数字应当写成1.05×10³，此时我们对最后的数字进行了舍去，即去掉了最后一位。如果去掉的数小于5，则不动前一位；如果去掉的数大于等于5，则前一位加1。这一规则称四舍五入，例如1054保留两位数字应写成1.1×10³。

某些人遵循四舍六入五成双的规则，例如15.45进舍至15.4，而15.55进舍至15.6。这种规则不带偏见，用于银行或大型数据系统。在计算中你会使用电子计算器，此时我们不需要在计算中途进行进舍，而是将结果储存在计算器中，并在写最终答案的时候使用正确的有效数字。注意：计算中使用科学常数或者进行进舍，至少需比最终结果多保留一位有效数字。

例题

执行以下计算，并保留正确的有效数字：

• (0.225 × 0.0035) ÷ (2.16×10²)
• (2.06×10²) + (1.32×10⁴) − (1.26×10³)

解答

第一个式子是乘除法运算，0.0035的有效数字位数最少（2位），因此答案保留两位有效数字，即3.6×10⁻⁶。第二个式子是加法运算，2.06×10²的末尾有效数字是个位，1.32×10⁴末位有效数字是百位，1.26×10³末位有效数字是十位，因此结果保留到百位，即1.47×10⁴。

练习

执行以下计算，并保留正确的有效数字：

$\frac{(1.302\times 10^3)+952.7}{(1.57\times 10^2)-12.22}$